Question

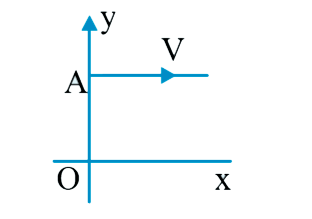
Statement - 1 : A particle moves with a constant velocity parallel to the x-axis. Its angular momentum w.r.t. the origin will remains constant.
Because
Statement - 2 : Angular momentum is defined as $\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{P}$

Options

A. Statement - 1 is true, statement - 2 is true, statement - 2 is correct explanation for statement - 1
B. Statement - 1 is true, Statement - 2 is true, Statement - 2 is not a correct explanation for statement - 1
C. statement - 1 is true, statement - 2 is false
D. statement - 1 is false, statement - 2 is true.

Answer

A

Explanation

To solve the problem, we need to analyze the two statements provided and understand the relationship between the motion of the particle and its angular momentum.

1. Understanding the Motion of the Particle:
- The particle is moving with a constant velocity parallel to the x-axis. This means that its speed and direction are not changing over time.

2. Defining Angular Momentum:
- Angular momentum (L) of a particle with respect to a point (in this case, the origin) is defined as:
\( \vec{L} = \vec{r} \times \vec{P} \)
- Here, \(\vec{r}\) is the position vector from the origin to the particle, and \(\vec{P}\) is the linear momentum of the particle, which is given by \(\vec{P} = m\vec{v}\), where \(m\) is the mass and \(\vec{v}\) is the velocity.

3. Analyzing the Angular Momentum:
- The magnitude of angular momentum can be expressed as:
\( L = mv r \sin(\theta) \)
- In this equation, \(r\) is the distance from the origin to the line of action of the velocity vector, and \(\theta\) is the angle between \(\vec{r}\) and \(\vec{v}\).

4. Constant Parameters:
- Since the particle is moving with constant velocity, both \(m\) (mass) and \(\vec{v}\) (velocity) are constant.
- The distance \(r\) from the origin to the line of action of the velocity vector remains constant as the particle moves parallel to the x-axis.

5. Conclusion on Angular Momentum:
- Since \(m\), \(v\), \(r\), and \(\theta\) remain constant throughout the motion, the angular momentum \(L\) will also remain constant. Therefore, Statement 1 is true.

6. Explanation of Statement 2:
- Statement 2 provides the definition of angular momentum, which supports the conclusion drawn in Statement 1. Thus, Statement 2 is a correct explanation for Statement 1.

Final Conclusion:
- Both statements are true, and Statement 2 is the correct explanation for Statement 1.

Answer:
- The answer is (A): Both statements are true, and Statement 2 is the correct explanation for Statement 1.

---