A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
56 g
66 g
76 g
86 g
The correct Answer is:b
Let m be the mass of the meter stick concentrated at C, the 50 cm mark as shown in the figure.
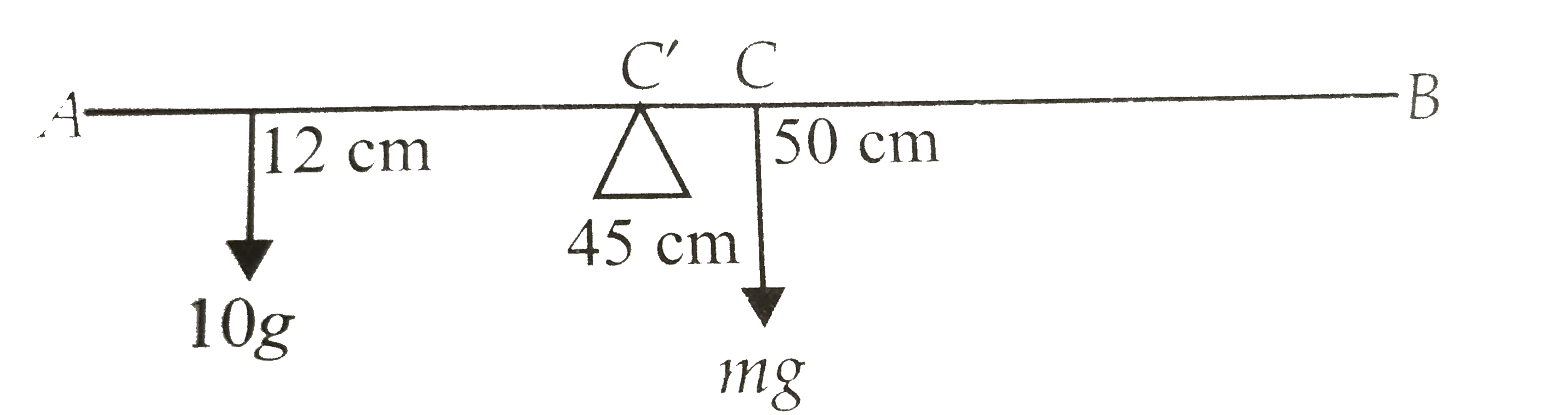
In Equilibrium, taking moments of forces about C′, we get
10g(45−12)=mg(50−45),10g×33=mg×5
m=10×335=66g
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOMENT OF INERTIA7videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - THEOREMS OF PERPENDICULAR AND PARALLEL AXES5videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - TORQUE AND ANGULAR MOMENTUM11videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on of the other at the 12cm mark, the stick is found to balanced at 45cm. The mass of the metre stick is.
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.View Solution
Knowledge Check
- Question 1 - Select One
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
A56 gB66 gC76 gD86 g - Question 2 - Select One
If the centre of gravity of a metre scale of mass 80g lies at the 45 cm mark, then which one of the following diagrams will show the balanced position of the scale.
A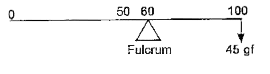
B
C
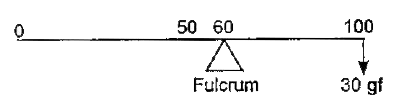D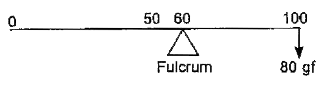
A uniform metre rule rests horizontally on a knife edge at the 60cm mark when a mass of 10g is suspended from one end. Draw a diagram of the arrangement.
(a) At which end must this mass be suspended
(b) What is the mass of the rule?
(c ) THe 10g mass is now shifted to the 90cm mark. In which direction must the knife edge be shifted to make the rule horizontal again?View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?View SolutionA metre stick is pivoted about its centre. A piece of wax of mass 20 g travelling horizontally and perpendicular to it at 5 m/s strikes and adheres to one end of the stick so that the stick starts to rotate in a horizontal circle. Given the moment of inertia of the stick and wax about the pivot is 0.02 kg m2, the initial angular velocity of the stick is :
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
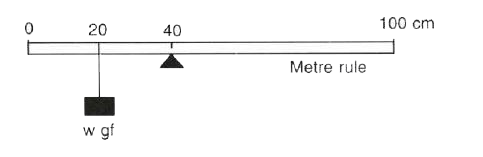
the resultant moment and its direction if the weight w is moved to the mark 30 cm.View SolutionA massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest
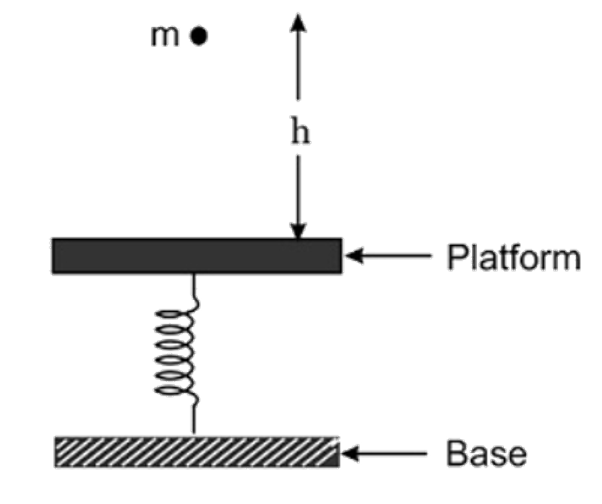
View SolutionA particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)
View Solution