A car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
4000 N on each front wheel, 5000 N on each back wheel
5000 N on each front wheel, 4000 N an each back wheel
4500 N on each wheel, 4500 N on each back wheel
3000 N on each front wheel, 6000 N on each back wheel
The correct Answer is:a
To solve the problem of determining the forces exerted by the level ground on each front wheel and each back wheel of the car, we can follow these steps:
Step 1: Write down the given data
- Mass of the car (m) = 1800 kg
- Distance between front and back axles (d) = 1.8 m
- Distance from the front axle to the center of gravity (h) = 1.05 m
- Gravitational acceleration (g) = 9.8 m/s²
Step 2: Calculate the total weight of the car
The weight (W) of the car can be calculated using the formula:
W=m⋅g
W=1800kg⋅9.8m/s2=17640N
Step 3: Set up the equations for equilibrium
Let Rf be the force exerted by the ground on the front wheels and Rb be the force on the back wheels. According to the equilibrium of forces:
Rf+Rb=W
Rf+Rb=17640N (Equation 1)
Step 4: Set up the torque equilibrium equation
Taking moments about the center of gravity (CG) to find the relationship between Rf and Rb:
- The distance from the center of gravity to the front axle is 1.05m.
- The distance from the center of gravity to the back axle is 1.8m−1.05m=0.75m.
Setting up the torque equilibrium about the center of gravity:
Rf⋅1.05=Rb⋅0.75
From this, we can express Rb in terms of Rf:
Rb=Rf⋅1.050.75
Rb=1.4Rf (Equation 2)
Step 5: Solve the equations simultaneously
Substituting Equation 2 into Equation 1:
Rf+1.4Rf=17640
2.4Rf=17640
Rf=176402.4=7350N
Now substituting Rf back into Equation 2 to find Rb:
Rb=1.4⋅7350=10290N
Step 6: Calculate the force on each wheel
Since the car has two front wheels and two back wheels:
- Force on each front wheel:
Force on each front wheel=Rf2=73502=3675N
- Force on each back wheel:
Force on each back wheel=Rb2=102902=5145N
Final Results
- Force on each front wheel = 3675 N
- Force on each back wheel = 5145 N
- Mass of the car (m) = 1800 kg
- Distance between front and back axles (d) = 1.8 m
- Distance from the front axle to the center of gravity (h) = 1.05 m
- Gravitational acceleration (g) = 9.8 m/s²
The weight (W) of the car can be calculated using the formula:
W=m⋅g
W=1800kg⋅9.8m/s2=17640N
Let Rf be the force exerted by the ground on the front wheels and Rb be the force on the back wheels. According to the equilibrium of forces:
Rf+Rb=W
Rf+Rb=17640N (Equation 1)
Taking moments about the center of gravity (CG) to find the relationship between Rf and Rb:
- The distance from the center of gravity to the front axle is 1.05m.
- The distance from the center of gravity to the back axle is 1.8m−1.05m=0.75m.
Rf⋅1.05=Rb⋅0.75
From this, we can express Rb in terms of Rf:
Rb=Rf⋅1.050.75
Rb=1.4Rf (Equation 2)
Substituting Equation 2 into Equation 1:
Rf+1.4Rf=17640
2.4Rf=17640
Rf=176402.4=7350N
Rb=1.4⋅7350=10290N
Since the car has two front wheels and two back wheels:
- Force on each front wheel:
Force on each front wheel=Rf2=73502=3675N
Force on each back wheel=Rb2=102902=5145N
- Force on each front wheel = 3675 N
- Force on each back wheel = 5145 N
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOMENT OF INERTIA7videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - THEOREMS OF PERPENDICULAR AND PARALLEL AXES5videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - TORQUE AND ANGULAR MOMENTUM11videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The distance between the inner and outer wheels of a car is 1.75 m and its centre of gravity is 0-50 m above the ground. What is the maximum speed with which the car can negotiate a curve of radius of 40 m without overturning ?
View SolutionFor a car taking a turn on a horizontal surface, let N1 and N2 be the normal reactions of the road on the inner and outer wheels respectively
View Solution
Knowledge Check
- Question 1 - Select One
A 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
A25√2 N, 203 NB50√2 N, 230 NC203 N, 25√2 ND230N,50√2 N
Two conductors each of length 12 m lie parallel to each other in air. The centre to center distance between two conductors is 15×10−2 m and the current in each conductor is 300 amperes. Determine the force in newton tending to pull the conductors together.
View SolutionThe dipole moment of a short bar magnet is 1.25A−m2. The magnetic field on its axis at a distance of 0.5 metre from the centre of the magnet is
View SolutionA 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
View SolutionA car travels from A to B and returns to its original position.
The distance between A and B is 2000 m.
The car takes 5 min to travel from A to B but takes 8 min to travel back from B to A. Is the speed of the car greater while going from A to B or while travelling back from B to A?View SolutionFigure shows a pulley of mass m and radius r with two blocks of masses m1 and m2 attached with a light and unstretchable string. Find the acceleration of the blocks, tensions in the string and the force exerted by the pulley on the celling from which it is hanging. Assume no slipping between the string and the wheel.
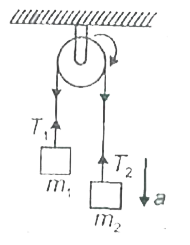 View Solution
View SolutionA bicycle is traveling downhill at a high speed. Suddenly, the cyclist sees that a bridge ahead has collapsed, so she has to stop. What is the maximum magnitude of acceleration the bicycle can have if it is not to flip over its front wheel—in particular, if its rear wheel is not to leave the ground? The slope makes an angle of 37∘ with the horizontal. On level ground, the centre of mass of the woman–bicycle system is at a point 1.0m above the ground, 1.0m horizontally behind the axle of the front wheel, and 35.0 cm in front of the rear axle. Assume that the tires do not skid.
View SolutionThe diameter of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at 24611 revolutions per minute. Find :
the revolutions per minute made by the front wheel.View Solution

