A hoop of radius 2m weight 100kg.It rolls along a horizontal floor so that its centre of mass has a speed of 20cms−1. How much work has to be done to stop it ?
2 J
4 J
6 J
8 J
The correct Answer is:b
To solve the problem of how much work has to be done to stop a hoop rolling along a horizontal floor, we can follow these steps:
Step 1: Identify the given data
- Radius of the hoop, R=2m
- Weight of the hoop (mass), m=100kg
- Speed of the center of mass, V=20cm/s=0.2m/s
Step 2: Calculate the angular speed (ω)
For a rolling object, the relationship between linear speed V and angular speed ω is given by:
ω=VR
Substituting the values:
ω=0.2m/s2m=0.1rad/s
Step 3: Calculate the kinetic energy
The total kinetic energy (KE) of the hoop consists of translational kinetic energy and rotational kinetic energy. The formulas for these are:
- Translational kinetic energy:
KEtrans=12mV2
- Rotational kinetic energy:
KErot=12Iω2
Where I is the moment of inertia of the hoop. For a hoop, the moment of inertia is:
I=mR2
Substituting this into the rotational kinetic energy formula gives:
KErot=12(mR2)ω2
Step 4: Substitute the values into the kinetic energy formulas
First, calculate the translational kinetic energy:
KEtrans=12×100kg×(0.2m/s)2=12×100×0.04=2J
Next, calculate the rotational kinetic energy:
KErot=12×(100kg×(2m)2)×(0.1rad/s)2
Calculating I:
I=100×4=400kg m2
Now substituting into the rotational kinetic energy:
KErot=12×400×(0.1)2=12×400×0.01=2J
Step 5: Calculate the total kinetic energy
Now, we can find the total kinetic energy:
KEtotal=KEtrans+KErot=2J+2J=4J
Step 6: Determine the work done to stop the hoop
According to the work-energy theorem, the work done to stop the hoop is equal to the total kinetic energy:
Work done=KEtotal=4J
Final Answer
The work that has to be done to stop the hoop is 4J.
---
- Radius of the hoop, R=2m
- Weight of the hoop (mass), m=100kg
- Speed of the center of mass, V=20cm/s=0.2m/s
For a rolling object, the relationship between linear speed V and angular speed ω is given by:
ω=VR
Substituting the values:
ω=0.2m/s2m=0.1rad/s
The total kinetic energy (KE) of the hoop consists of translational kinetic energy and rotational kinetic energy. The formulas for these are:
- Translational kinetic energy:
KEtrans=12mV2
- Rotational kinetic energy:
KErot=12Iω2
Where I is the moment of inertia of the hoop. For a hoop, the moment of inertia is:
I=mR2
Substituting this into the rotational kinetic energy formula gives:
KErot=12(mR2)ω2
First, calculate the translational kinetic energy:
KEtrans=12×100kg×(0.2m/s)2=12×100×0.04=2J
KErot=12×(100kg×(2m)2)×(0.1rad/s)2
Calculating I:
I=100×4=400kg m2
Now substituting into the rotational kinetic energy:
KErot=12×400×(0.1)2=12×400×0.01=2J
Now, we can find the total kinetic energy:
KEtotal=KEtrans+KErot=2J+2J=4J
According to the work-energy theorem, the work done to stop the hoop is equal to the total kinetic energy:
Work done=KEtotal=4J
The work that has to be done to stop the hoop is 4J.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - HOTS HIGHER ORDER THINKING SKILL
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCER EXAMPLAR PROBLEMS
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ANGULAR MOMENTUM IN CASE OF ROTATIONS ABOUT A FIXED AXIS
16 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
The mass of a hoop of radius 0.30 m is 2kg. It rolls along a horizontal floor so that its centre of mass has a speed of 2 m/s. What is the work done to stop it ?
View SolutionA disc of radius 2 m and mass 100kg rolls on a horizontal floor, its centre of mass has speed of 20cm/s. How much work is needed to stop it ?
View Solution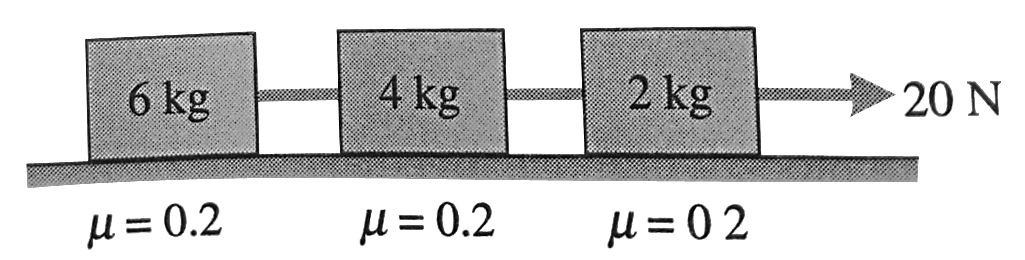
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA uniform sphere of mass 200 g rolls without slipping on a plane surface so that its centre moves at a speed of 2.00 cm/s. Find its kinetic energy.
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform sphere of mass 500g rolls without slipping on a plane surface so that its centre moves at a speed of 0.02m/s.
The total kinetic energy of rolling sphere would be (in J)
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View Solution
