The relation between the slope of isothemal curve and slope of adiabatic curve
a. slope of adiabatic curve =γ times slope of isotharmal curve
b.slope of isothermal curve =γ times slope of adiabatic curve
c.slope of adiabatic curve =γ2 times slope of isothermal curve
d. slope of isothermal curve =γ2 times slope of adiabatic curve
The correct Answer is:A
To find the relation between the slope of the isothermal curve and the slope of the adiabatic curve, we can follow these steps:
Step 1: Understand the Isothermal Process
For an isothermal process, the product of pressure (P) and volume (V) is constant. This can be expressed mathematically as:
PV=constant
Step 2: Differentiate the Isothermal Equation
Differentiating the equation PV=constant gives:
VdP+PdV=0
Rearranging this, we find:
VdP=−PdV
Thus, we can express the slope dPdV as:
dPdV=−PV
This is our Equation 1.
Step 3: Understand the Adiabatic Process
For an adiabatic process, the relationship can be expressed as:
PVγ=constant
where γ is the heat capacity ratio (C_p/C_v).
Step 4: Differentiate the Adiabatic Equation
Differentiating the equation PVγ=constant gives:
VγdP+γPVγ−1dV=0
Rearranging this, we find:
VγdP=−γPVγ−1dV
Thus, we can express the slope dPdV as:
dPdV=−γPV
This is our Equation 2.
Step 5: Compare the Slopes
Now, we have the slopes for both processes:
- Isothermal: dPdV=−PV (Equation 1)
- Adiabatic: dPdV=−γPV (Equation 2)
From these equations, we can see that:
dPdV (adiabatic)=γ×dPdV (isothermal)
Conclusion
Thus, the slope of the adiabatic curve is γ times the slope of the isothermal curve.
Final Answer
The relation between the slope of the isothermal curve and the slope of the adiabatic curve is:
slope of adiabatic curve=γ×slope of isothermal curve
For an isothermal process, the product of pressure (P) and volume (V) is constant. This can be expressed mathematically as:
PV=constant
Differentiating the equation PV=constant gives:
VdP+PdV=0
Rearranging this, we find:
VdP=−PdV
Thus, we can express the slope dPdV as:
dPdV=−PV
This is our Equation 1.
For an adiabatic process, the relationship can be expressed as:
PVγ=constant
where γ is the heat capacity ratio (C_p/C_v).
Differentiating the equation PVγ=constant gives:
VγdP+γPVγ−1dV=0
Rearranging this, we find:
VγdP=−γPVγ−1dV
Thus, we can express the slope dPdV as:
dPdV=−γPV
This is our Equation 2.
Now, we have the slopes for both processes:
- Isothermal: dPdV=−PV (Equation 1)
- Adiabatic: dPdV=−γPV (Equation 2)
dPdV (adiabatic)=γ×dPdV (isothermal)
Thus, the slope of the adiabatic curve is γ times the slope of the isothermal curve.
The relation between the slope of the isothermal curve and the slope of the adiabatic curve is:
slope of adiabatic curve=γ×slope of isothermal curve
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs8videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason15videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason15videos
UNITS AND MEASUREMENTS
Similar Questions
Find the relation between the slopes of marginal revenue curve and the average revenue curve, for the demand function p = a - bx
View SolutionIf the slope for isotherm is X and the slope for adiabat is Y then
View SolutionShow that the slope of adiabatic curve at any point is Yama times the slope of an isothermal curve at the corresponding point.
View SolutionThe activity of a certain radioactive sample is plotted against time in graph. If the initial slope of the curve is m, then find the slope of the curve at point P ?
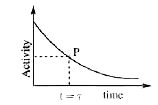 View Solution
View SolutionStatement-1: Temperature of a system can be increased without supplying heat.
Statement-2: If the initial volume of system is equal to final volume in a process then work done is necessarily zero.
Statement-3: If an adiabatic curve for a gas intersect with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is γ.View SolutionWrite the slope of the normal to the curve y=1x at the point (3,13)
View SolutionFor a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
View SolutionA curve in the first quadrant is such that the slope of OP is twice the slope of the tangent drawn at P to the curve, where O is the origin and P is any general point on the curve. If the curve passes through (4, 2), then its equation is
View SolutionFind the slope of the tangent and the normal to the curve y=x3−x at x=2
View SolutionFind the slopes of the tangent and the normal to the curve y=√x at x=9
View Solution

