Statement-1: Temperature of a system can be increased without supplying heat.
Statement-2: If the initial volume of system is equal to final volume in a process then work done is necessarily zero.
Statement-3: If an adiabatic curve for a gas intersect with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is γ.
FTF
TFT
TFF
TTT
The correct Answer is:B
To analyze the three statements provided in the question, we will evaluate each statement one by one based on the principles of thermodynamics.
Step 1: Evaluate Statement 1
Statement 1: "Temperature of a system can be increased without supplying heat."
- In thermodynamics, an adiabatic process is one in which no heat is exchanged with the surroundings (Q = 0).
- According to the first law of thermodynamics:
Q=ΔU+W
If Q=0, then:
0=ΔU+W⟹ΔU=−W
- Here, ΔU is the change in internal energy, and W is the work done on the system. If work is done on the system (compression), then W is negative, which means ΔU is positive, leading to an increase in temperature.
- Therefore, it is possible to increase the temperature of a system without supplying heat by doing work on it.
Conclusion: Statement 1 is True.
Step 2: Evaluate Statement 2
Statement 2: "If the initial volume of a system is equal to final volume in a process then work done is necessarily zero."
- Work done in a thermodynamic process is given by the area under the pressure-volume (P-V) curve.
- If the initial and final volumes are the same, it does not necessarily mean that the work done is zero. For example, in a cyclic process like the Carnot cycle, the system may return to the same volume but still perform work during the intermediate steps.
- Therefore, even if the initial and final volumes are the same, work can be done in the process.
Conclusion: Statement 2 is False.
Step 3: Evaluate Statement 3
Statement 3: "If an adiabatic curve for a gas intersects with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is gamma."
- For an adiabatic process, the equation is given by:
PVγ=constant
Differentiating gives the slope:
dPdV=−γPV
- For an isothermal process, the equation is given by:
PV=constant
Differentiating gives the slope:
dPdV=−PV
- To find the ratio of the slopes at the point of intersection:
Ratio=slope of adiabaticslope of isothermal=−γPV−PV=γ
- This confirms that the ratio of the slopes at the intersection point is indeed gamma.
Conclusion: Statement 3 is True.
Final Summary:
- Statement 1: True
- Statement 2: False
- Statement 3: True
Answer:
The correct answer is that Statement 1 and Statement 3 are true, while Statement 2 is false.
---
Statement 1: "Temperature of a system can be increased without supplying heat."
- According to the first law of thermodynamics:
Q=ΔU+W
If Q=0, then:
0=ΔU+W⟹ΔU=−W
- Here, ΔU is the change in internal energy, and W is the work done on the system. If work is done on the system (compression), then W is negative, which means ΔU is positive, leading to an increase in temperature.
- Therefore, it is possible to increase the temperature of a system without supplying heat by doing work on it.
Statement 2: "If the initial volume of a system is equal to final volume in a process then work done is necessarily zero."
- If the initial and final volumes are the same, it does not necessarily mean that the work done is zero. For example, in a cyclic process like the Carnot cycle, the system may return to the same volume but still perform work during the intermediate steps.
- Therefore, even if the initial and final volumes are the same, work can be done in the process.
Statement 3: "If an adiabatic curve for a gas intersects with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is gamma."
PVγ=constant
Differentiating gives the slope:
dPdV=−γPV
- For an isothermal process, the equation is given by:
PV=constant
Differentiating gives the slope:
dPdV=−PV
- To find the ratio of the slopes at the point of intersection:
Ratio=slope of adiabaticslope of isothermal=−γPV−PV=γ
- This confirms that the ratio of the slopes at the intersection point is indeed gamma.
- Statement 1: True
- Statement 2: False
- Statement 3: True
The correct answer is that Statement 1 and Statement 3 are true, while Statement 2 is false.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-I) Subjective Type
5 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-J) Aakash Challengers Questions
6 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-G) Integer Answer Type Questions
3 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
The final volume of a system is equal to the initial volume in a certain process. Is the work done by the system necessarily zero? Is it necessarily nonzero?
View SolutionTwo moles of a gas expand reversibly and isothermally at temperature of 300K. Initial volume of the gas is 1 L while the final pressure is 4.926 atm . The work done by gas is
View Solution
Knowledge Check
Two different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
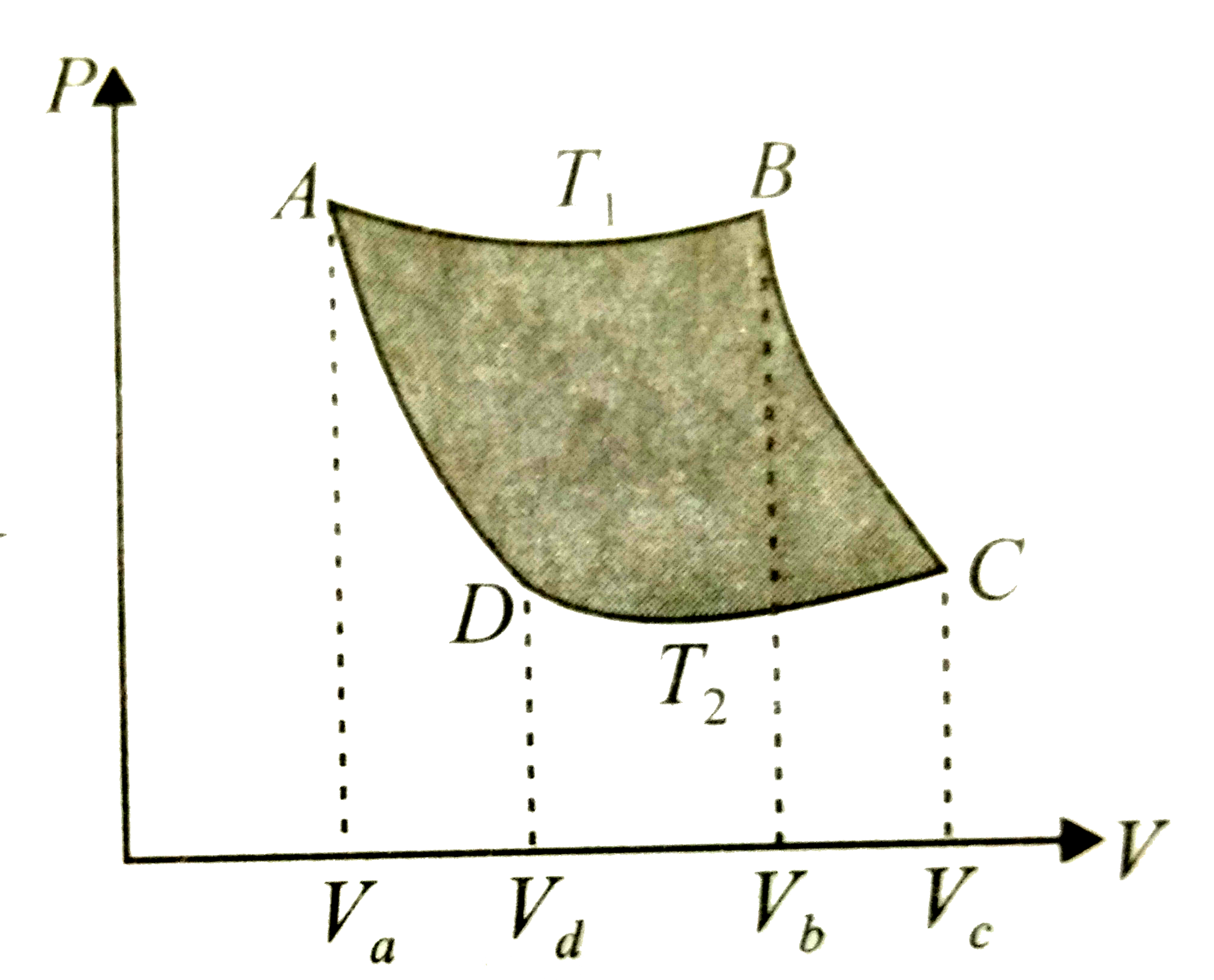 Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Statement-1: The amount of work done in the isothermal expansion is greater than work done in the adiabatic system for same final volume.
Statement-2: In the adiabatic expansion of a gas temperature and pressure both decrease due to decrease in internal energy of the system.
View SolutionRMS speed of a monoatomic gas is increased by 2 times. If the process is done adiabatically then the ratio of initial volume to final volume will be
View SolutionStatement-1: If the pressure and temperature of a gas sample are doubled then the volume of the gas will remain unchanged.
Statement-2: Molar specific heat for an adiabatic process is zero.
Statement-3: Heat energy is a path function.
View SolutionStatement-1: For a gaseous system Cp is always greater than Cv
Statement-2: Work done by a gas at constant volume is zero.
View SolutionIn adiabatic expansion of monoatomic ideal gas, if volume increases by 24% then pressure decreases by 40%.
Statement-2 : For adiabatic process PVγ = constant
View SolutionStatement-1: Two gases at same pressure, volume & temperature are compressed to same volume. The first isothermally and second adiabatically, greater work is done on the gas for an adiabatic process.
Statement-2: Final temperature for gas going under isothermal process is more than gas going under adiabatic process.
View SolutionStatement-1 : In an adiabatic process, change in internal energy of a gas is equal to work done on/by the gas in the process.
Statement-2 : This is because temp.of gas remains constant in an adiabatic process.
View Solution
