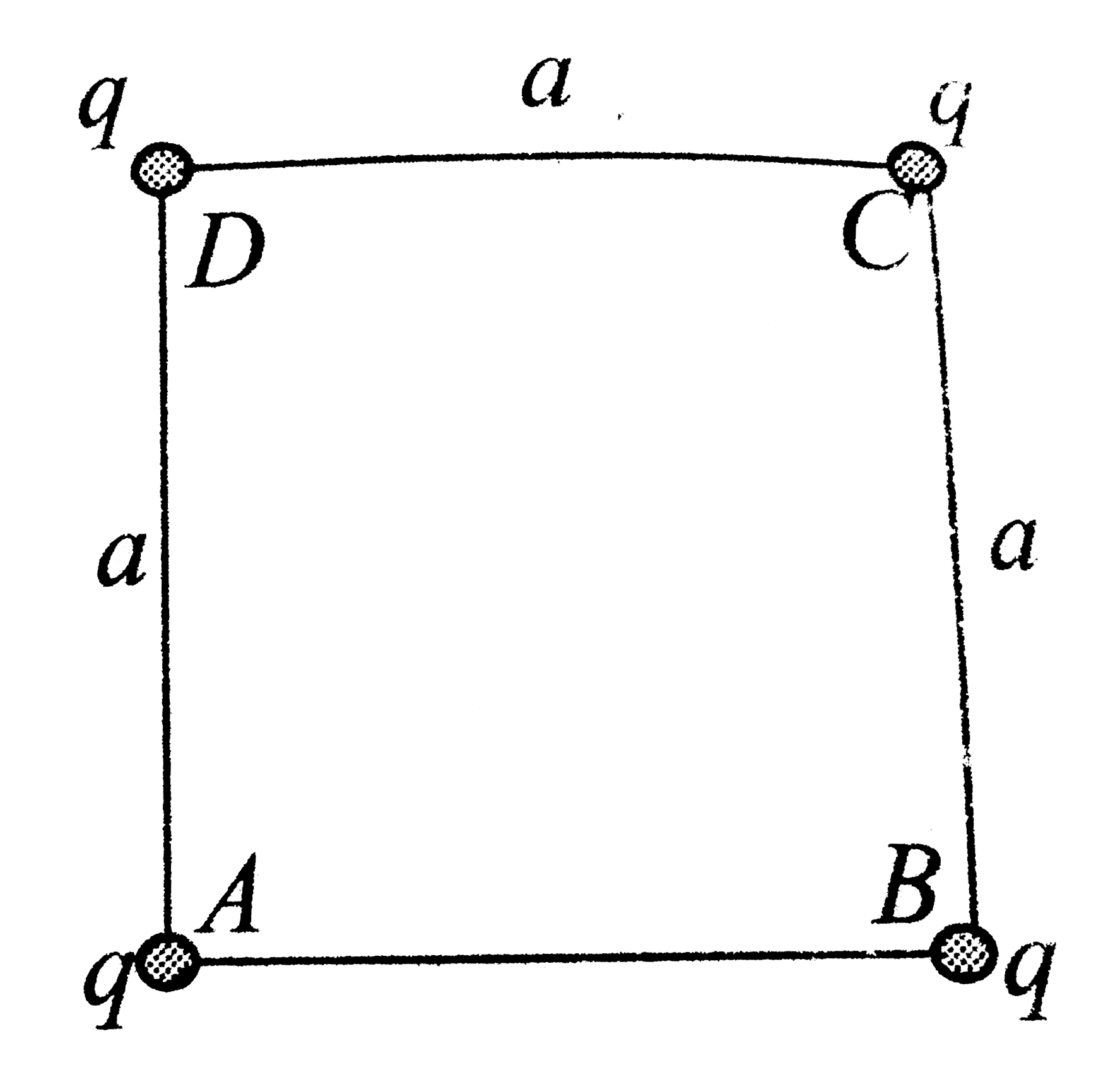
Four equal charges are placed at the four corners of a square of each side is 'a'. Work done in removing a charge from its centre to infinity is
zero
The correct Answer is:B
To solve the problem of calculating the work done in removing a charge −Q from the center of a square with four equal charges Q at its corners, we can follow these steps:
Step 1: Understand the Configuration
We have four equal charges Q placed at the corners of a square with side length a. We need to find the work done in moving a charge −Q from the center of the square to infinity.
Step 2: Determine the Initial Potential Energy
The potential energy \( U \) at a point due to a charge is given by the formula:
\(
U = k \frac{Q_1 Q_2}{r}
\)
where \( k \) is Coulomb's constant, \( Q_1 \) and \( Q_2 \) are the magnitudes of the charges, and \( r \) is the distance between them.
Step 3: Calculate the Distance from the Center to a Corner
The distance from the center of the square to any corner can be calculated using the Pythagorean theorem. The distance \( r \) from the center to a corner is:
\(
r = \frac{a}{\sqrt{2}}
\)
Step 4: Calculate the Total Potential at the Center
Since there are four charges, the total potential \( V \) at the center due to these four charges is:
\(
V = k \left( \frac{Q}{r} + \frac{Q}{r} + \frac{Q}{r} + \frac{Q}{r} \right) = 4k \frac{Q}{r}
\)
Substituting \( r = \frac{a}{\sqrt{2}} \):
\(
V = 4k \frac{Q}{\frac{a}{\sqrt{2}}} = \frac{4\sqrt{2}kQ}{a}
\)
Step 5: Calculate the Initial Potential Energy
The initial potential energy \( U_i \) of the charge −Q at the center is given by:
\(
U_i = V \cdot (-Q) = -Q \cdot \frac{4\sqrt{2}kQ}{a} = -\frac{4\sqrt{2}kQ^2}{a}
\)
Step 6: Determine the Work Done
The work done \( W \) in moving the charge −Q from the center to infinity is equal to the negative of the initial potential energy (since potential energy at infinity is zero):
\(
W = -U_i = \frac{4\sqrt{2}kQ^2}{a}
\)
Step 7: Substitute the Value of \( k \)
Using \( k = \frac{1}{4\pi\epsilon_0} \):
\(
W = \frac{4\sqrt{2} \cdot \frac{1}{4\pi\epsilon_0} Q^2}{a} = \frac{\sqrt{2}Q^2}{\pi\epsilon_0 a}
\)
Final Answer
Thus, the work done in removing the charge −Q from the center of the square to infinity is:
\(
W = \frac{\sqrt{2}Q^2}{\pi\epsilon_0 a}
\)
We have four equal charges Q placed at the corners of a square with side length a. We need to find the work done in moving a charge −Q from the center of the square to infinity.
The potential energy \( U \) at a point due to a charge is given by the formula:
\(
U = k \frac{Q_1 Q_2}{r}
\)
where \( k \) is Coulomb's constant, \( Q_1 \) and \( Q_2 \) are the magnitudes of the charges, and \( r \) is the distance between them.
The distance from the center of the square to any corner can be calculated using the Pythagorean theorem. The distance \( r \) from the center to a corner is:
\(
r = \frac{a}{\sqrt{2}}
\)
Since there are four charges, the total potential \( V \) at the center due to these four charges is:
\(
V = k \left( \frac{Q}{r} + \frac{Q}{r} + \frac{Q}{r} + \frac{Q}{r} \right) = 4k \frac{Q}{r}
\)
Substituting \( r = \frac{a}{\sqrt{2}} \):
\(
V = 4k \frac{Q}{\frac{a}{\sqrt{2}}} = \frac{4\sqrt{2}kQ}{a}
\)
The initial potential energy \( U_i \) of the charge −Q at the center is given by:
\(
U_i = V \cdot (-Q) = -Q \cdot \frac{4\sqrt{2}kQ}{a} = -\frac{4\sqrt{2}kQ^2}{a}
\)
The work done \( W \) in moving the charge −Q from the center to infinity is equal to the negative of the initial potential energy (since potential energy at infinity is zero):
\(
W = -U_i = \frac{4\sqrt{2}kQ^2}{a}
\)
Using \( k = \frac{1}{4\pi\epsilon_0} \):
\(
W = \frac{4\sqrt{2} \cdot \frac{1}{4\pi\epsilon_0} Q^2}{a} = \frac{\sqrt{2}Q^2}{\pi\epsilon_0 a}
\)
Thus, the work done in removing the charge −Q from the center of the square to infinity is:
\(
W = \frac{\sqrt{2}Q^2}{\pi\epsilon_0 a}
\)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Four identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
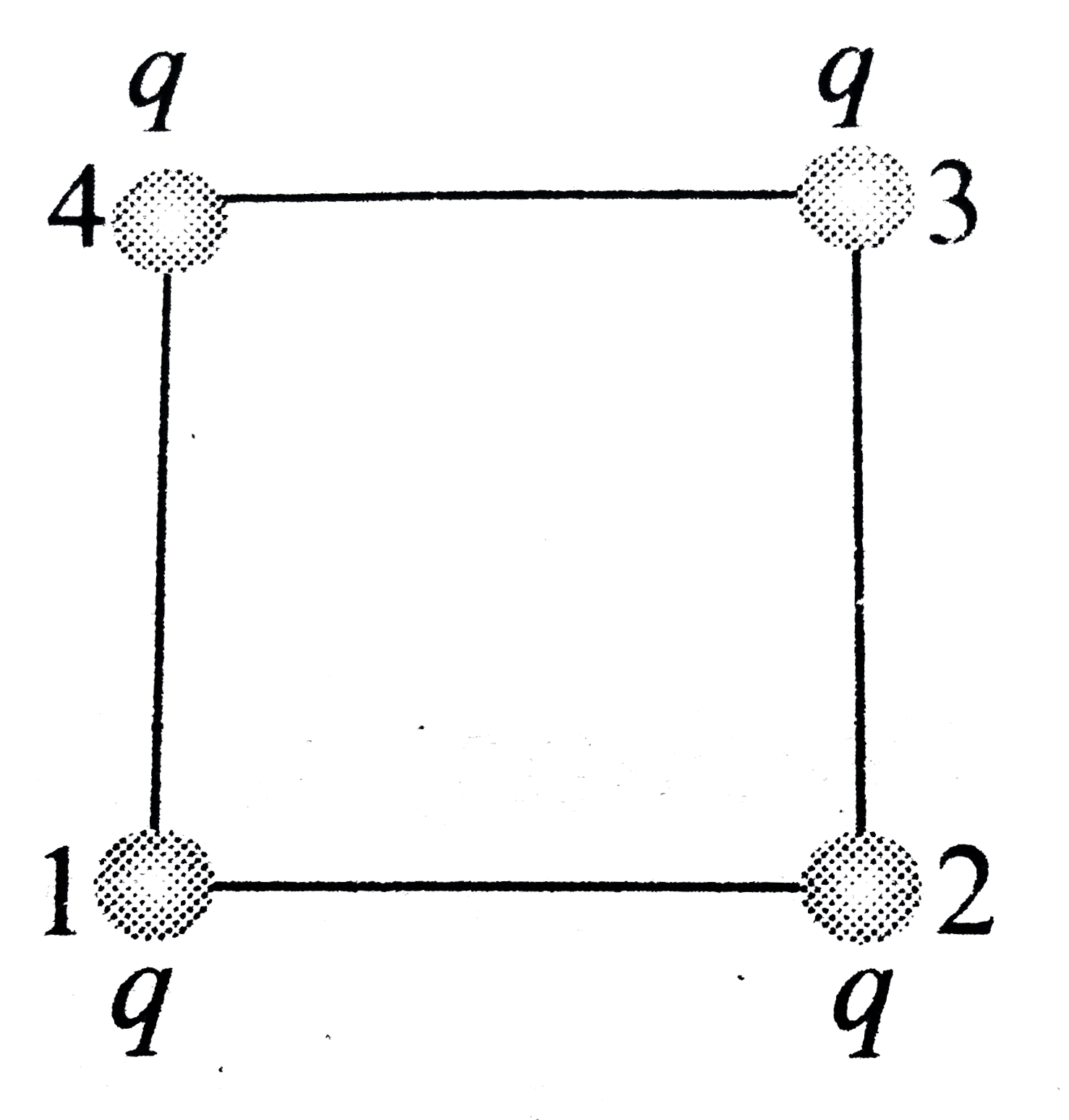 .
.
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
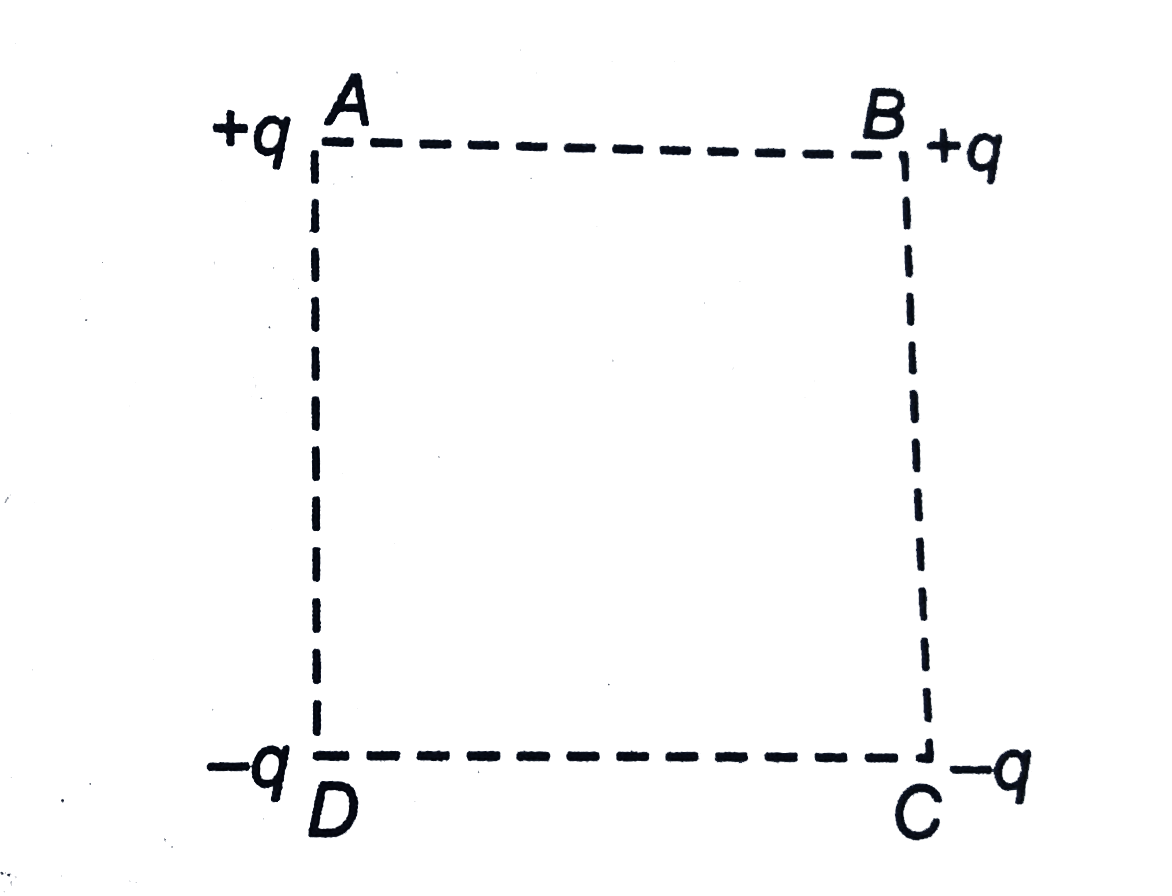
View SolutionFor charges A,B,C and D are plasced at the four corners of a squre of a side a. The energy required to take the charges C and D to infinity (they are also infinitely separated from each other )is
View SolutionFour bodies each of mass m are placed at the different corners of a square of side a. find the work done on the system to take any one body to infinity.
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
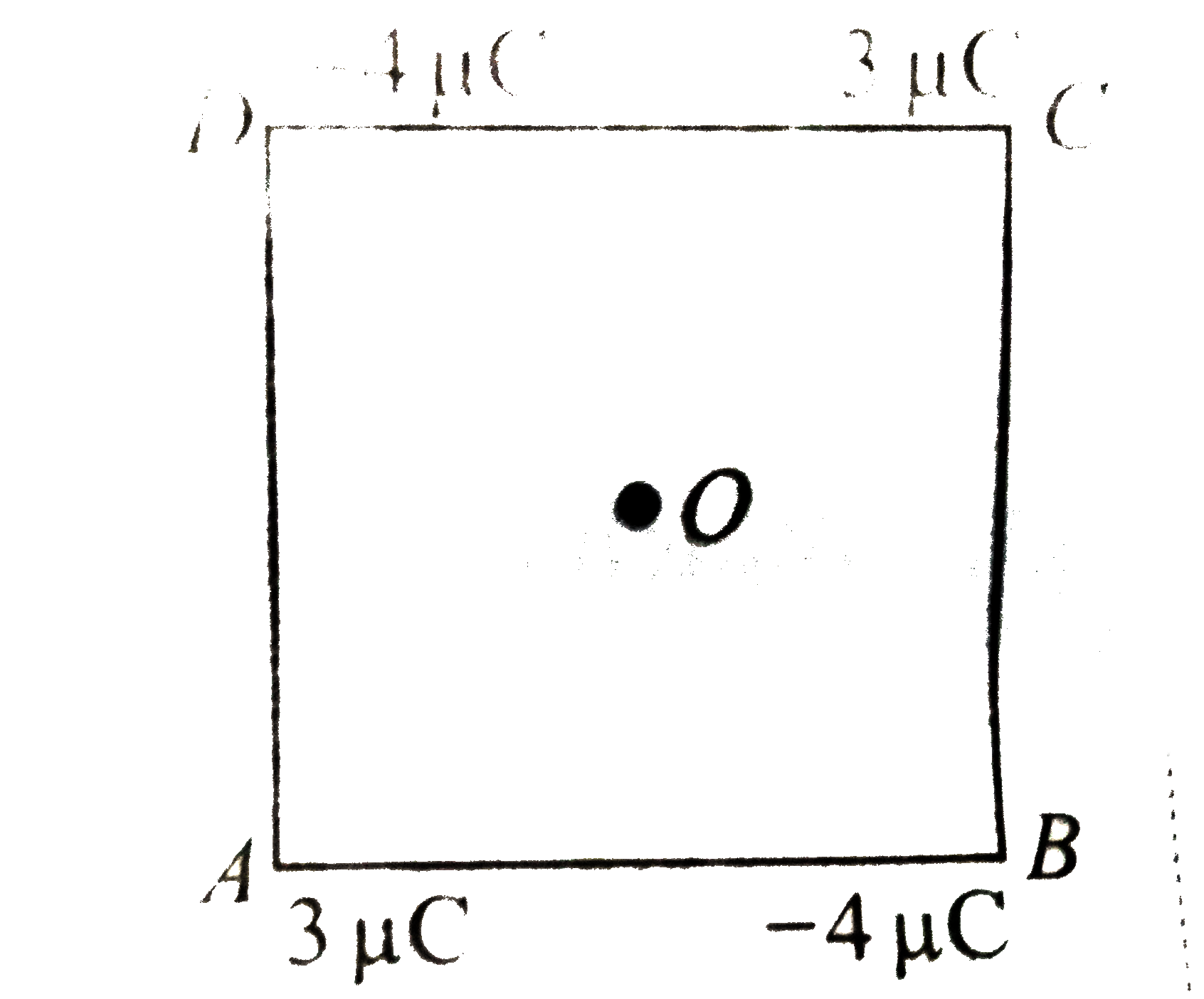
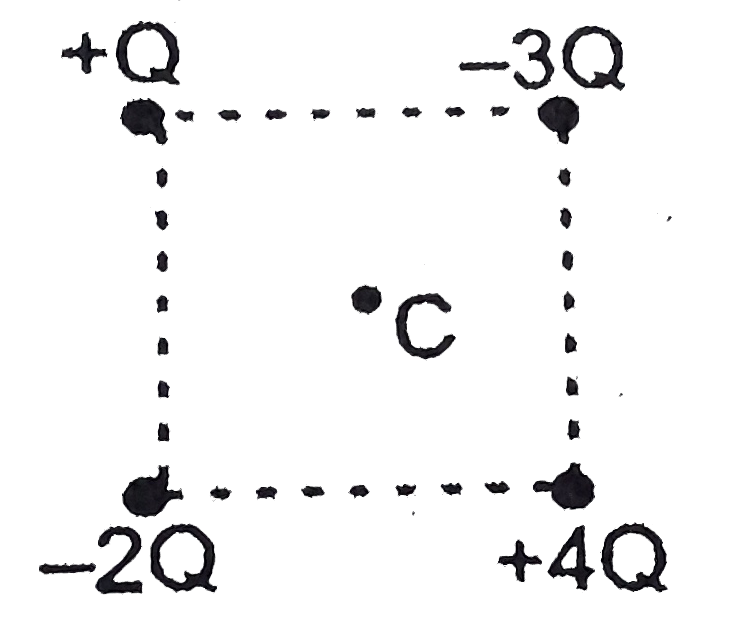
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
View SolutionFour equal electric charges are arranged at the four corners of a square of side 'a'. Out of these four charges, two charges are positive and placed at the ends of one diagonal. The other two charges are positive and placed at the ends of the other diagonal. The energy of the system in
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View Solution
