Two moving coil metres M1andM2 have the following particular R1=10Ω,N1=30,A1=3.6×10−3m2,B1=0.25T,
R2=14Ω,N2=42,A2=1.8×10−3m2,B2=0.50T
The spring constants are identical for the two metres. What is the ratio of current sensitivity and voltage sensitivity of M2 toM1?
1.4, 1
1.4, 0
2.8, 2
2.8, 0
The correct Answer is:A
To find the ratio of current sensitivity and voltage sensitivity of meters M2 to M1, we can follow these steps:
Step 1: Understand the formulas for current sensitivity and voltage sensitivity
The formulas for current sensitivity (Is) and voltage sensitivity (Vs) are given by:
- Current sensitivity:
Is=N⋅B⋅Ak
- Voltage sensitivity:
Vs=N⋅B⋅Ak⋅R
Where:
- N = number of turns
- B = magnetic field strength
- A = area of the coil
- k = spring constant
- R = resistance
Step 2: Calculate the current sensitivity for both meters
For meter M1:
Is1=N1⋅B1⋅A1k=30⋅0.25⋅3.6×10−3k
For meter M2:
Is2=N2⋅B2⋅A2k=42⋅0.50⋅1.8×10−3k
Step 3: Find the ratio of current sensitivities
Now, we can find the ratio of current sensitivities:
Is2Is1=42⋅0.50⋅1.8×10−3k30⋅0.25⋅3.6×10−3k=42⋅0.50⋅1.830⋅0.25⋅3.6
Calculating the above expression:
=42⋅0.50⋅1.830⋅0.25⋅3.6=42⋅0.930⋅0.9=4230=1.4
Step 4: Calculate the voltage sensitivity for both meters
For meter M1:
Vs1=N1⋅B1⋅A1k⋅R1=30⋅0.25⋅3.6×10−3k⋅10
For meter M2:
Vs2=N2⋅B2⋅A2k⋅R2=42⋅0.50⋅1.8×10−3k⋅14
Step 5: Find the ratio of voltage sensitivities
Now, we can find the ratio of voltage sensitivities:
Vs2Vs1=42⋅0.50⋅1.8k⋅1430⋅0.25⋅3.6k⋅10=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14
Notice that the k cancels out:
=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14=1
Final Ratios
Thus, the final ratios are:
- Ratio of current sensitivity Is2Is1=1.4
- Ratio of voltage sensitivity Vs2Vs1=1
The formulas for current sensitivity (Is) and voltage sensitivity (Vs) are given by:
- Current sensitivity:
Is=N⋅B⋅Ak
- Voltage sensitivity:
Vs=N⋅B⋅Ak⋅R
Where:
- N = number of turns
- B = magnetic field strength
- A = area of the coil
- k = spring constant
- R = resistance
For meter M1:
Is1=N1⋅B1⋅A1k=30⋅0.25⋅3.6×10−3k
Is2=N2⋅B2⋅A2k=42⋅0.50⋅1.8×10−3k
Now, we can find the ratio of current sensitivities:
Is2Is1=42⋅0.50⋅1.8×10−3k30⋅0.25⋅3.6×10−3k=42⋅0.50⋅1.830⋅0.25⋅3.6
Calculating the above expression:
=42⋅0.50⋅1.830⋅0.25⋅3.6=42⋅0.930⋅0.9=4230=1.4
For meter M1:
Vs1=N1⋅B1⋅A1k⋅R1=30⋅0.25⋅3.6×10−3k⋅10
Vs2=N2⋅B2⋅A2k⋅R2=42⋅0.50⋅1.8×10−3k⋅14
Now, we can find the ratio of voltage sensitivities:
Vs2Vs1=42⋅0.50⋅1.8k⋅1430⋅0.25⋅3.6k⋅10=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14
Notice that the k cancels out:
=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14=42⋅0.50⋅1.8⋅1030⋅0.25⋅3.6⋅14=1
Thus, the final ratios are:
- Ratio of current sensitivity Is2Is1=1.4
- Ratio of voltage sensitivity Vs2Vs1=1
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
Two moving coil meters M1 and M2 have the following particulars:
R1=10Ω, N1=30, A1=3⋅6×10−3m2, B1=0⋅25T,
R2=14Ω, N2=42, A2=1⋅8×10−3m2, B2=0⋅50T
(The spring constants are identical for the two metres). Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M2 and M1.View SolutionIn the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?
 View Solution
View SolutionIn each case m1=4kg and m2=3kg. If a1 and a2 and a3 are the respective acceleration of the block m1 in given situation, then
 View Solution
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
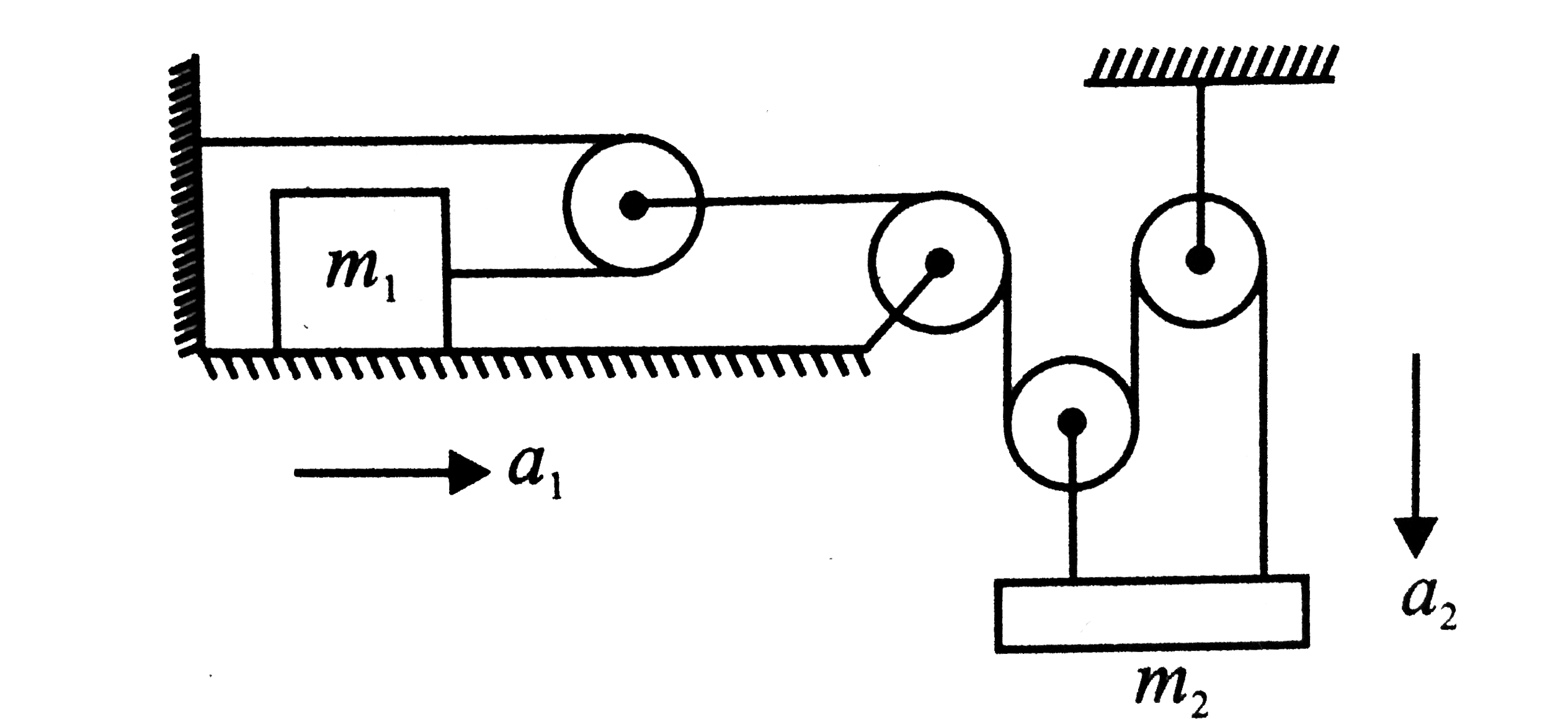 View Solution
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionThe following concentration were obtained for the formation of NH3 from N2andH2 at equilibrium for the reaction N2(g)+3H2(g)⇔2NH3(g)
[N2]=1.5×10−2M
[H2]=3.0×10−2M
[NH3]=1.2×10−2M
Calculate equilibrium constant.View SolutionFrom the following sets of quantum numbers , state which are possible ?
(i) n=0,l=0,ml=1,ms=+1/2
(ii) n=2,l=1,ml=0,ms=−1/2
(iii) n=2,l=0,m1=3,ms=+1/2
(iv) n=3,l=1,ml=0,ms=+1/2View SolutionFrom the point of the view of significant figures which of the following statements are correct ?
(i) 10.2cm+8cm=18.2cm
(ii) 2.53m−1.2m=1.33m
(iii) 4.2m×1.4m=5.88m2
(iv) 3.6m/1.75sec=2.1m/sView SolutionObserve the following reaction, 2A+B→C The rate of formation of C is 2.2×10−3 M m in−1. What is the value of −d[A]dt(in moL−1 m in −1) ?
View Solution

