A galvanometer of resistance 50Ω is connected to a battery of 3V along with resistance of 2950Ω in series. A full scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 20 division the above series resistance should be
6050Ω
4450Ω
5050Ω
5550Ω
The correct Answer is:B
To solve the problem, we need to determine the series resistance required to reduce the deflection of the galvanometer from 30 divisions to 20 divisions. Here's the step-by-step solution:
Step 1: Calculate the initial current (I_G) for full-scale deflection
The total resistance in the circuit when the galvanometer shows full-scale deflection (30 divisions) is the sum of the galvanometer resistance (R_G) and the series resistance (R_S):
Rtotal=RG+RS=50Ω+2950Ω=3000Ω
Using Ohm's Law, the current (I_G) through the galvanometer can be calculated as:
IG=VRtotal=3V3000Ω=1×10−3A=1mA
Step 2: Calculate the current (I') for reduced deflection
To find the current required for 20 divisions, we can set up a proportion based on the full-scale deflection:
I′=IG30×20=1×10−3A30×20=23×10−3A=23mA
Step 3: Set up the equation for the new total resistance
The voltage across the circuit remains the same (3 V). Using Ohm's Law again for the new current (I'):
V=I′×Rnew
Where Rnew is the new total resistance. Thus,
3V=(23×10−3A)×Rnew
Rearranging gives:
Rnew=3V(23×10−3A)=3×32×10−3=4500Ω
Step 4: Calculate the required series resistance
The new total resistance (4500 Ω) includes the galvanometer resistance (50 Ω). Therefore, the required series resistance (R_S') is:
R′S=Rnew−RG=4500Ω−50Ω=4450Ω
Conclusion
The series resistance that should be connected to reduce the deflection to 20 divisions is 4450 Ω.
---
The total resistance in the circuit when the galvanometer shows full-scale deflection (30 divisions) is the sum of the galvanometer resistance (R_G) and the series resistance (R_S):
To find the current required for 20 divisions, we can set up a proportion based on the full-scale deflection:
The voltage across the circuit remains the same (3 V). Using Ohm's Law again for the new current (I'):
The new total resistance (4500 Ω) includes the galvanometer resistance (50 Ω). Therefore, the required series resistance (R_S') is:
The series resistance that should be connected to reduce the deflection to 20 divisions is 4450 Ω.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A galvanometer of resistance 50Ω is connected to a battery of 3V along with a resistance of 2950Ω in series. A full scale deflection of 30 division is obtained in the galvanometer. In order to reduce this deflection to 20 division, the resistance in series should be:-
View SolutionA galvanometer of resistance 50Ω is connected to a battery of 8 V along with a resistance of 3950Ω in series. A full scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 15 divisions, the resistance in series should be .... Ω.
View Solution
Knowledge Check
- Question 1 - Select One
A galvanometer of resistance 25Ω is connected to a battery of 2 volt along with a resistance in series. When the value of this resistance is 3000Ω, a full scale deflection of 30 units is obtained in the galvanometer. In order to reduce this deflection to 20 units, the resistance in series will be
A4512ΩB5413ΩC2000ΩD6000Ω
A galvanometer of resistance 30Ω is connected to a battery of emf 2 V with 1970Ω resistance in series. A full scale deflection of 20 divisions is obtained in the galvanometer. To reduce the deflection to 10 divisions, the resistance in series required is
View SolutionA galvanometer of 50Ω resistance when connected across the terminals of a battery of emf 2V along with the resistance 200Ω the deflection produced in the galvanometer is 10 divisions. If the total number of divisions on the galvanometer ·scale on either side of central zero is 30, then the maximum current that can pass through the galvanometer is
View SolutionA galvanometer having internal resistance 10Ω required 0.01 A for a full scale deflection. To convert this galvanometer to a voltmeter of full scale deflection at 120 V, we need to connect a resistance of
View SolutionTo measure the resistance of a galvanometer by half deflection method, a shunt is connected to the galvanometer . The shunt is
View SolutionA galvanometer of resistance 50Ω is converted into an ammeter by connecting a low resistance (shunt) of value 1Ω in parallel to the galvanometer, S. If full - scale deflection current of the galvanometer is 10 mA, then the maximum current that can be measured by the ammeter is -
View SolutionA galvanometer has resistance 1Ω. Maximum deflection current through it is 0.1 A
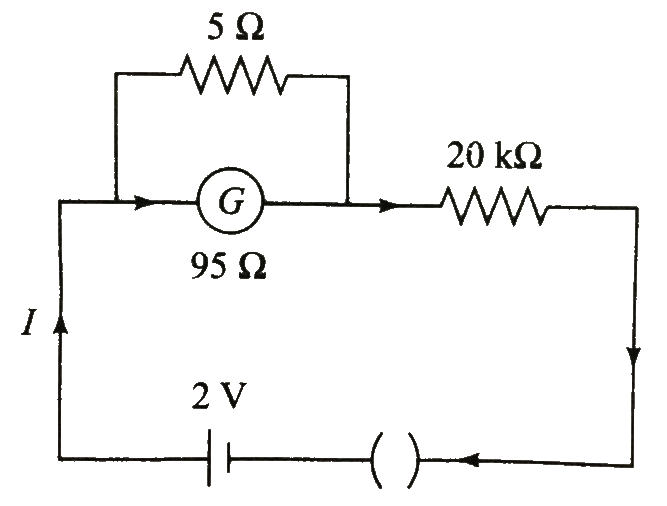
View SolutionA galvanometer of resistance 95Ω, shunted resistance of 5Ω, gives a deflection of 50 divisions when joined in series with a resistance of 20kΩ and a 2V accumulator. What is the current sensitivity of the galvanomter (in div/μA)?
 View Solution
View Solution

