An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
The electron will be accelerated along the axis.
The electron path will be circular about the axis.
The electron will experience a force at 45∘ to the axis and hence execute a helical path.
The electron will contnue to move with uniform velocity along the axis of the solenoid.
The correct Answer is:D
To solve the problem, we need to analyze the situation of an electron moving through a current-carrying solenoid. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the setup
We have a long solenoid carrying a current, which creates a magnetic field inside it. The electron is projected with a uniform velocity along the axis of the solenoid.
Hint: Remember that the magnetic field inside a long solenoid is uniform and directed along the axis of the solenoid.
Step 2: Determine the direction of the magnetic field
The magnetic field (B) inside a long solenoid is directed along the axis of the solenoid. For a solenoid with current flowing in a certain direction, the magnetic field lines run parallel to the axis of the solenoid.
Hint: Use the right-hand rule to determine the direction of the magnetic field based on the direction of the current in the solenoid.
Step 3: Apply the Lorentz force law
The force (F) experienced by a charged particle moving in a magnetic field is given by the Lorentz force law:
F=Q(V×B)
where:
- Q is the charge of the particle,
- V is the velocity vector of the particle,
- B is the magnetic field vector.
Hint: Remember that the charge of the electron is negative, and that the cross product will depend on the angle between the velocity and the magnetic field.
Step 4: Analyze the angle between velocity and magnetic field
In this case, the electron is moving along the axis of the solenoid, which means the angle (θ) between the velocity vector (V) and the magnetic field vector (B) is 0 degrees.
Hint: Recall that the sine of 0 degrees is 0, which will affect the calculation of the force.
Step 5: Calculate the force
Using the formula:
F=QVBsin(θ)
Since θ=0:
F=QVBsin(0)=0
Thus, the force acting on the electron is zero.
Hint: Consider what happens to an object when no net force acts upon it.
Step 6: Conclusion about the motion of the electron
Since the force acting on the electron is zero, according to Newton's first law of motion, the electron will continue to move with uniform velocity along the axis of the solenoid.
Hint: Think about the implications of Newton's first law in the context of motion with no net external force.
Final Answer
The correct option is: The electron will continue to move with uniform velocity along the axis of the solenoid.
We have a long solenoid carrying a current, which creates a magnetic field inside it. The electron is projected with a uniform velocity along the axis of the solenoid.
The magnetic field (B) inside a long solenoid is directed along the axis of the solenoid. For a solenoid with current flowing in a certain direction, the magnetic field lines run parallel to the axis of the solenoid.
The force (F) experienced by a charged particle moving in a magnetic field is given by the Lorentz force law:
F=Q(V×B)
where:
- Q is the charge of the particle,
- V is the velocity vector of the particle,
- B is the magnetic field vector.
In this case, the electron is moving along the axis of the solenoid, which means the angle (θ) between the velocity vector (V) and the magnetic field vector (B) is 0 degrees.
Using the formula:
F=QVBsin(θ)
Since θ=0:
F=QVBsin(0)=0
Thus, the force acting on the electron is zero.
Since the force acting on the electron is zero, according to Newton's first law of motion, the electron will continue to move with uniform velocity along the axis of the solenoid.
The correct option is: The electron will continue to move with uniform velocity along the axis of the solenoid.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION & REASON15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Magnetic Force15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A proton is projected with a uniform velocity 'v' along the axis of a current carrying solenoid, then
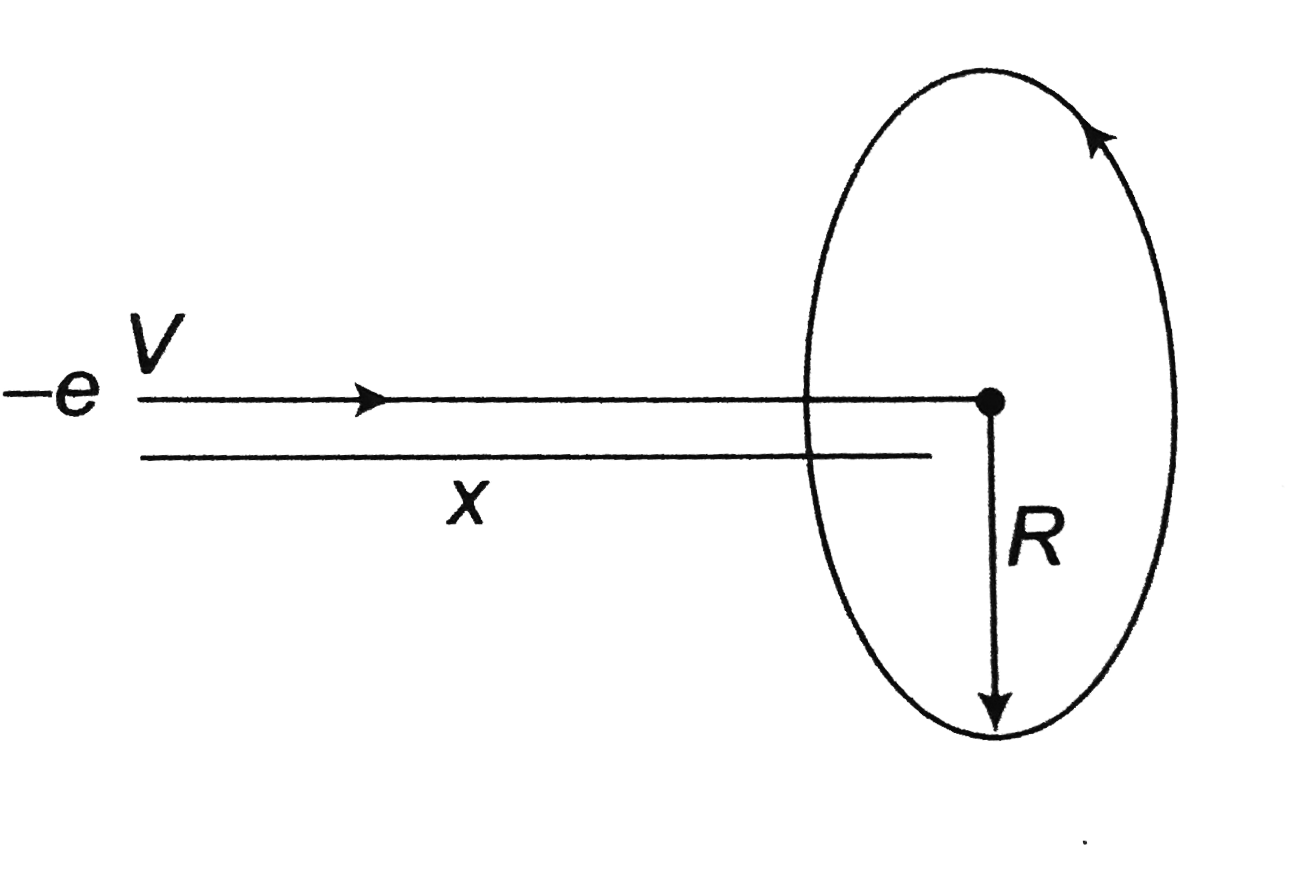
View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a disc rotates with uniform angular velocity, which of the following is not true ?
Aa. The sense of rotation remains same.Bb. The orientation of the axis of rotation remains same.Cc. The speed of rotation is non-zero and remains same.Dd. The angular acceleration is non-zero and remains same.
In a current carrying long solenoid, the field produced does not depend upon
View SolutionMagnetic lines of force inside a current carrying solenoid are
View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
View SolutionDraw magnetic field lines in and around a current carrying straight solenoid.
View SolutionThe strength of magnetic field inside a long current-carrying straight solenoid is:
View SolutionTwo infinite long wires, each carrying current I, are lying along x- and y-axis, respectively. A charged particle, having a charge q and mass m, is projected with a velocity u along the straight line OP. The path of the particle is (neglect gravity)
 View Solution
View Solution

