The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?
0.35atms−1
2.235×10−3atms−1
7.8×10−4atms−1
1.55×10−4atms−1
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Reaction
The reaction given is the thermal decomposition of SO2Cl2 into SO2 and Cl2:
SO2Cl2(g)→SO2(g)+Cl2(g)
This is a first-order reaction.
Step 2: Analyze the Data
We have the following data from the experiments:
- Experiment 1: Time = 0 s, Total Pressure = 0.5 atm
- Experiment 2: Time = 100 s, Total Pressure = 0.6 atm
Step 3: Determine Initial Pressure
The initial pressure P0 can be determined from the first experiment, which is:
P0=0.5atm
Step 4: Calculate the Rate Constant k
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P02P0−Pt)
Where:
- Pt is the total pressure at time t.
- For the second experiment, t=100s and Pt=0.6atm.
Substituting the values:
k=2.303100log(0.52×0.5−0.6)
Calculating the denominator:
2×0.5−0.6=1−0.6=0.4
Now substituting:
k=2.303100log(0.50.4)
Calculating the logarithm:
log(0.50.4)=log(1.25)≈0.09691
Now substituting back:
k=2.303100×0.09691≈0.00223s−1
Step 5: Calculate the Rate of Reaction at Pt=0.65atm
Using the relationship for the rate of reaction:
Rate=k⋅PSO2Cl2
Where:
PSO2Cl2=2P0−Pt
Substituting Pt=0.65atm:
PSO2Cl2=2×0.5−0.65=1−0.65=0.35atm
Now substituting k and PSO2Cl2 into the rate equation:
Rate=0.00223⋅0.35≈0.0007805atm/s
Converting to scientific notation:
Rate≈7.805×10−4atm/s
Final Answer
The rate of reaction when the total pressure is 0.65 atm is approximately:
Rate≈7.81×10−4atm/s
---
The reaction given is the thermal decomposition of SO2Cl2 into SO2 and Cl2:
SO2Cl2(g)→SO2(g)+Cl2(g)
This is a first-order reaction.
We have the following data from the experiments:
- Experiment 1: Time = 0 s, Total Pressure = 0.5 atm
- Experiment 2: Time = 100 s, Total Pressure = 0.6 atm
The initial pressure P0 can be determined from the first experiment, which is:
P0=0.5atm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P02P0−Pt)
Where:
- Pt is the total pressure at time t.
- For the second experiment, t=100s and Pt=0.6atm.
k=2.303100log(0.52×0.5−0.6)
Calculating the denominator:
2×0.5−0.6=1−0.6=0.4
Now substituting:
k=2.303100log(0.50.4)
Calculating the logarithm:
log(0.50.4)=log(1.25)≈0.09691
Now substituting back:
k=2.303100×0.09691≈0.00223s−1
Using the relationship for the rate of reaction:
Rate=k⋅PSO2Cl2
Where:
PSO2Cl2=2P0−Pt
Substituting Pt=0.65atm:
PSO2Cl2=2×0.5−0.65=1−0.65=0.35atm
Now substituting k and PSO2Cl2 into the rate equation:
Rate=0.00223⋅0.35≈0.0007805atm/s
Converting to scientific notation:
Rate≈7.805×10−4atm/s
The rate of reaction when the total pressure is 0.65 atm is approximately:
Rate≈7.81×10−4atm/s
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Higher Order Thinking Skills9videos
CHEMICAL KINETICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT EXEMPLAR PROBLEMS17videos
CHEMICAL KINETICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Assertion And Reason15videos
BIOMOLECULES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - NCERT Exemplar15videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The following data were obtained during the first order thermal decompostion of SO2CI2 at a constant volume :
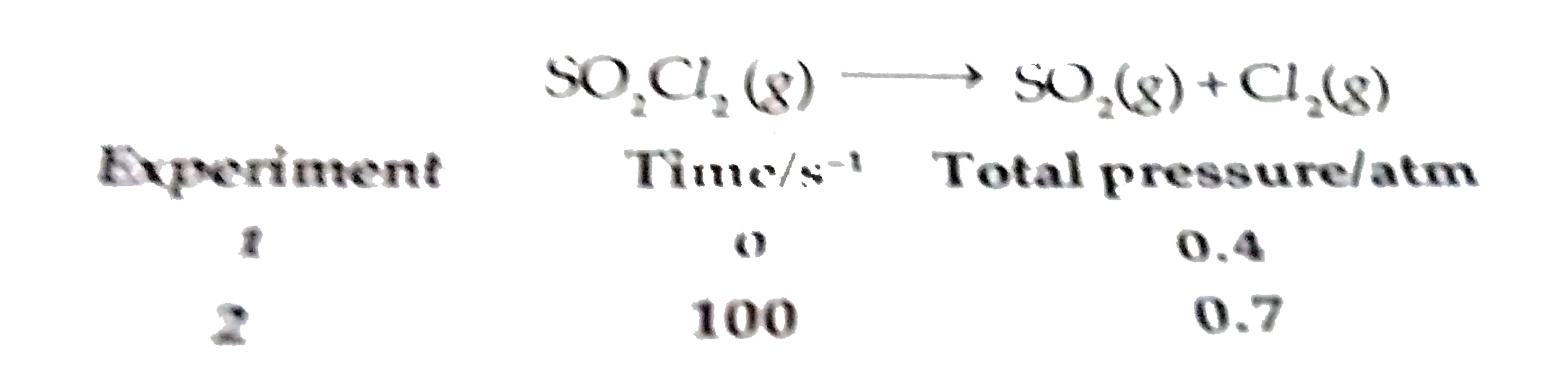
Calculate rate constantView SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g)→SO2(g)+Cl2(g)

What is the rate of reaction when total pressure of 0.65 atm?View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
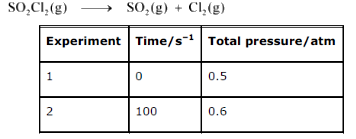
Calculate the rate of the reaction when total pressure is 0.65 atmView SolutionThe following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume :
2N2O5(g)→2N2O4(g)+O2(g)

Calculate the rate constant.View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at constant volume :
ExperimentTime (s)Total Pressure (atm)100.321000.5
Calculate rate constant
[Given : log 6 = 0.7782, log 3 = 0.4771]View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant
( given : log 4=0.6021,log2=0.3010)View Solution

