How does Ampere-Maxwell law explain the flow of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.

Text Solution

Verified by Experts

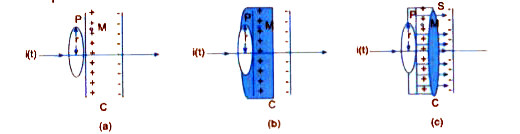
Consider charging of a parallel plate capacitor by a time-varying current iw Let us find the magnetic field at a point P in a region outside the capacitor. For this we consider a plane circular loop of radius r whose plane is perpendicular to the direction of the current carrying wire and which is centred symmetrically with respect to the wire [Fig]. Using symmetry condition and applying Ampere.s circuital law, we have
$B (2 π r) = μ_{0} i_{(t)} ....(i)$
However, if we consider a different surface, having the same boundary [either as shown in Fig. or Fir. and apply Ampere.s circuital law as before, we find
$B (2 π r) = μ_{0} (0) = 0 ....(ii)$
It is because nocurrent passes through the surface of Figs. and 8.04. It causes a contradiction because we get a finite value of magnetic field B by doing calculation in one way and zero value of B by doing calculation in another way. To remove this contradiction Maxwell introduced the concept of displacement current

$i_{D} = \in_{0} \frac{d ϕ_{E}}{d t},$ where $\frac{d ϕ_{E}}{d t}$ is the rate of change of electric flux between the plates of given capacitor.
Now, the Ampere - Maxwell.s circuital law is expressed as
$\oint \to B . \to d l = μ_{0} [i_{(t)} + i_{D}]$
Thus, Ampere - Maxwell law successfully explains the flow the current through a capacitor when it is being charged (or discharged) by a battery.

Updated on:21/07/2023

An amperes is a rate of flow of electric current of
Aone faraday per second
Bone coulomb per second
Cone coulomb per minutes
Done faraday per minutes
Assertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge
Reason : The displacement current arises in the region in which the electric field is constant with time.
AIf both assertion and reason are true and reason is the correct explanation of assertion
BIf both assertion and reason are true but reason is not the correct explanation of assertion
CIf assertion is true but reason is false
DIf both assertion and reason are false
Assertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge
Reason : The displacement current arises in the region in which the electric field is constant with time.
AIf both assertion and reason are true and reason is the correct explanation of assertion
BIf both assertion and reason are true but reason is not the correct explanation of assertion
CIf assertion is true but reason is false
DIf both assertion and reason are false