Considering the case of a parallel plate capacitor being charged, show how one is required to generalise Ampere.s circuital law to include the term due to displacement current.
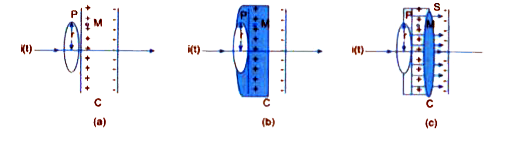
Consider charging of a parallel plate capacitor by a time-varying current iw Let us find the magnetic field at a point P in a region outside the capacitor. For this we consider a plane circular loop of radius r whose plane is perpendicular to the direction of the current carrying wire and which is centred symmetrically with respect to the wire [Fig]. Using symmetry condition and applying Ampere.s circuital law, we have
B(2πr)=μ0i(t) ....(i)
However, if we consider a different surface, having the same boundary [either as shown in Fig. or Fir. and apply Ampere.s circuital law as before, we find
B(2πr)=μ0(0)=0 ....(ii)
It is because nocurrent passes through the surface of Figs. and 8.04. It causes a contradiction because we get a finite value of magnetic field B by doing calculation in one way and zero value of B by doing calculation in another way. To remove this contradiction Maxwell introduced the concept of displacement current
iD=∈0dϕEdt, where dϕEdt is the rate of change of electric flux between the plates of given capacitor.
Now, the Ampere - Maxwell.s circuital law is expressed as
∮→B.→dl=μ0[i(t)+iD]
Thus, Ampere - Maxwell law successfully explains the flow the current through a capacitor when it is being charged (or discharged) by a battery.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER QUESTIONS-I
11 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION A)(MULTIPLE CHOICE QUESTIONS)
5 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - VERY SHORT ANSWER QUESTIONS
35 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)
4 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
Similar Questions
Considering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacment current.
View SolutionConsidering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law of include the term due to displacement current.
View Solution
Knowledge Check
The capacity of a parallel plate air capacitor is 2μF and voltage beteen the plates is changing at the rate of 3 v/s the displacement current in the capacitor is
A2μAB3μAC5μAD6μAThe capacity of a parallel plate air capacitor is 2μF and voltage beteen the plates is changing at the rate of 3 v/s the displacement current in the capacitor is
A2μAB3μAC5μAD6μAThe voltage between the plates of a parallel plate capacitor of capacitance 1μF is changing at the rate of 8 V/s. What is the displacement current in the capacitor?
A3μAB8μAC5μAD10μA
A parallel plate capacitor is being charged by a time varrying current. Explain briefly how Ampere's circutal law is generalised to incorporate the effect due to the displacement current.
View SolutionTwo circular plates of radius 0.1m are used to from a parallel plate capacitor. If displacement current between the plates is 2π.ampere, then find m agnetic filed produced by displacement current 4 cm from the axis of the plates.
View SolutionTwo circular plates of radius 0.1m are used to from a parallel plate capacitor. If displacement current between the plates is 2π.ampere, then find m agnetic filed produced by displacement current 4 cm from the axis of the plates.

View SolutionThe voltage between the plates of a parallel plate capacitor of capacitance 2μF is changing at the rate of 4V/s. What is the displacement current in the capacitor?
View SolutionThe voltage between the plates of a parallel plate capacitor of capacitance 1μF is changing at the rate of 4V/s. What is the displacement current in the capacitor?
View Solution
