When an object is placed at a distance of 25cm from a mirror, the magn

When an object is placed at a distance of 25 cm from a mirror, the magnification is $m_{1}$ . But the magnification becomes my, when the object is moved 15 cm farther away with respect to the earlier position. If $\frac{m_{1}}{m_{2}}$ =4 then find the focal length of the mirror and what type of mirror it is?
A20 cm, convex
B20 cm, concave
C10 cm, convex
D10 cm, concave
Consider a concave mirror and a convex lens (refractive index 1.5) of focal length $10 c m$ each separated by a distance of $50 c m$ in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of $15 c m$ from the mirror. Its erect image formed by this combination has magnification $M_{1}$ . When this set up is kept in a medium of refractive index $7 / 6$ , the magnification becomes $M_{2}$ . The magnitude $(\frac{M_{2}}{M_{1}})$ is :
.
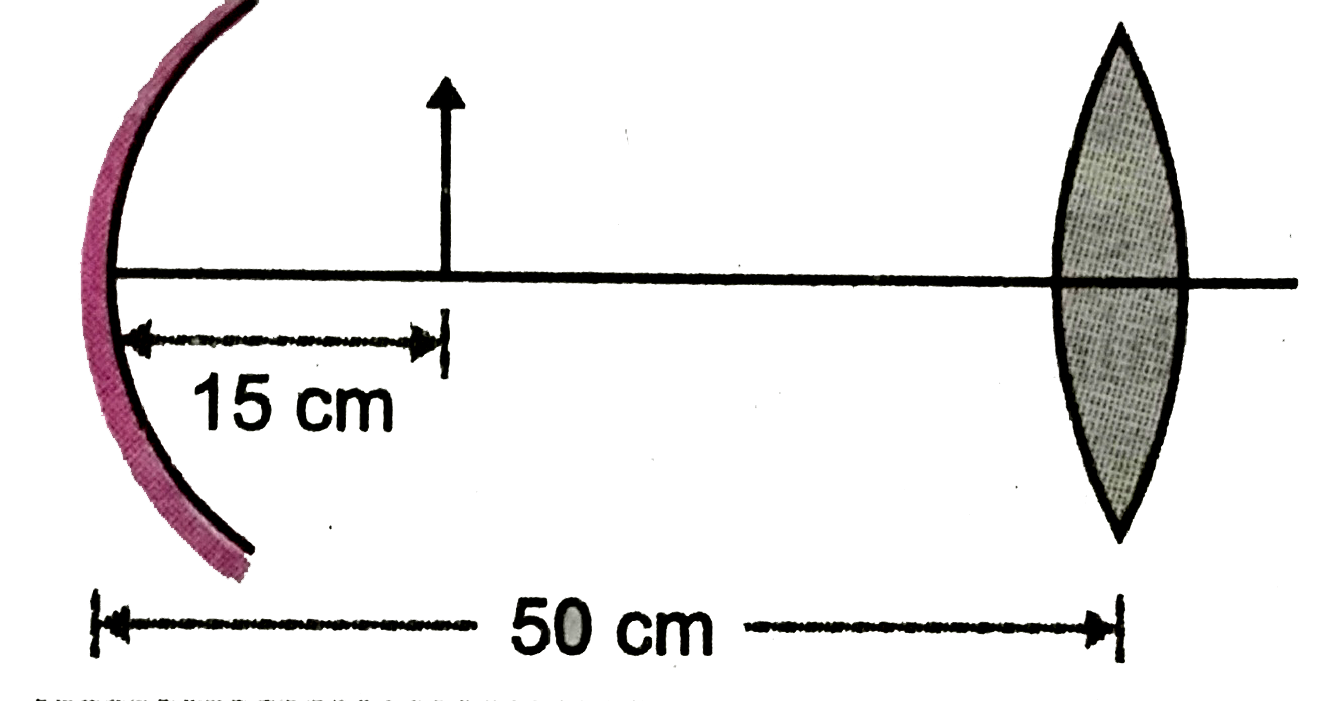A5
B6
C7
D8
An object is placed at a distance of 30 cm from the pole of a curved (convex or concave) mirror of focal length 15 cm. Then the linear magnification is
Aone for both types of mirrors
Bone only for a convex mirror
Cone only for a concave mirror
D $\frac{1}{3}$ for a concave mirror

When an object is placed at a distance of 25cm from a mirror, the magnification is $m_{1}$ . The object is moved 15 cm farther away with respect to the earlier position, and the magnification becomes $m_{2}$ . If $\frac{m_{1}}{m_{2}}$ = 4, then calculate the focal length of the mirror.