A point source S is placed at a height h from the bottom of a vessel of height H(< h) and area A. The vessel is polished at the base. Water is gradually filled in the vessel at a constant rate αm3/s. Find how the distance d of image of the source from the bottom of the vessel varies with time t.

d=μh−(μ−1)0aA
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
37 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
6 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - II
31 Videos
Similar Questions
A point source S is placed at a height h from the bottom of a vessel of height H(<h). The vessel is polished at the base. Water is polished at the base. Water is gradually filled in the vessel at a constant rate αm3/s. The distance d of image of the source after reflection from mirror from the bottom of the vessel varies with time t as
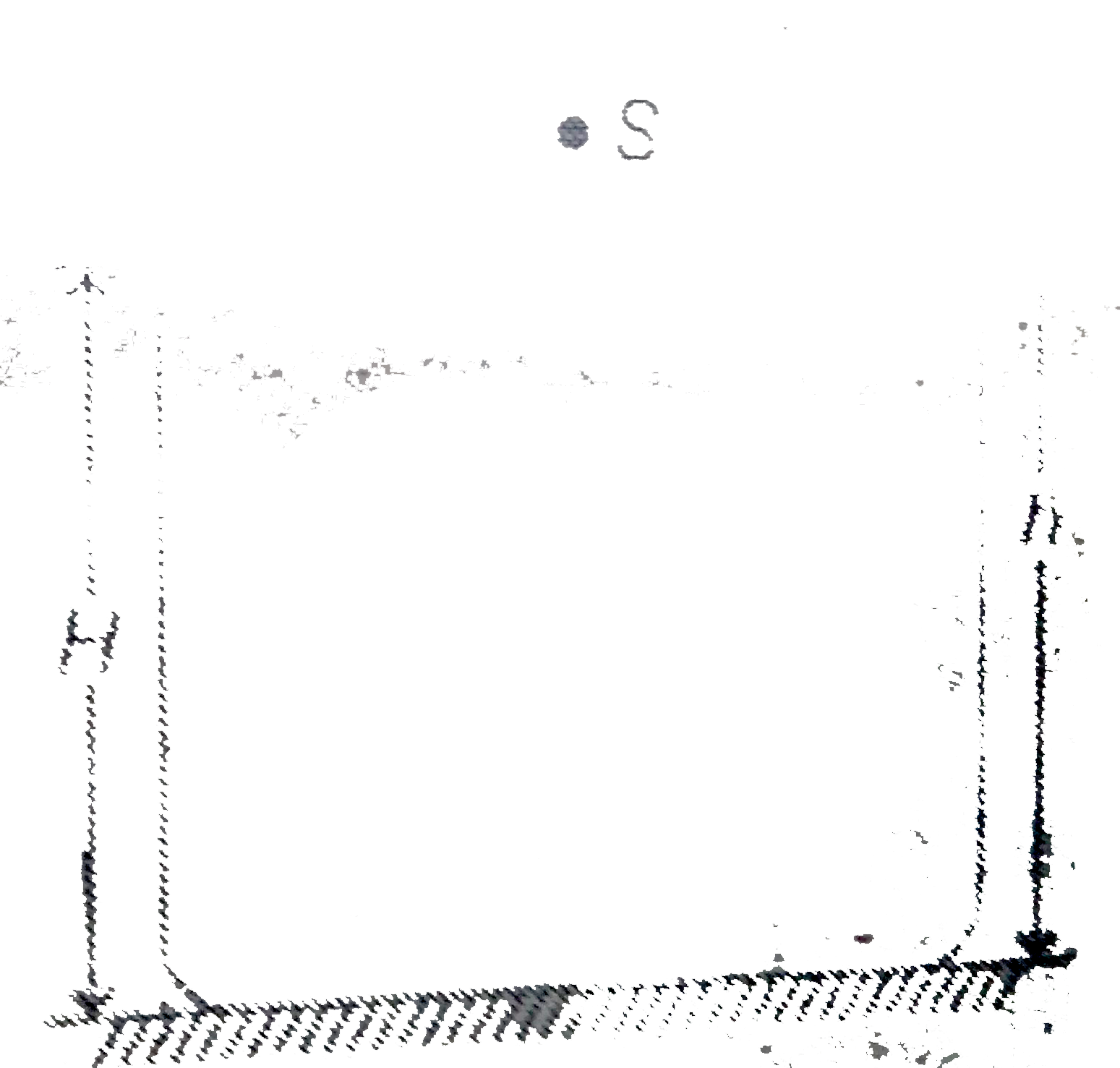
View SolutionWater is being poured in a vessel at a constant rate αm2/s. There is a small hole of area a at the bottom of the tank. The maximum level of water in the vessel is proportional to
View Solution
Knowledge Check
A point source S is placed at a height h from the bottom of a vessel of height H(<h). The vessel is polished at the base. Water is polished at the base. Water is gradually filled in the vessel at a constant rate αm3/s. The distance d of image of the source after reflection from mirror from the bottom of the vessel varies with time t as
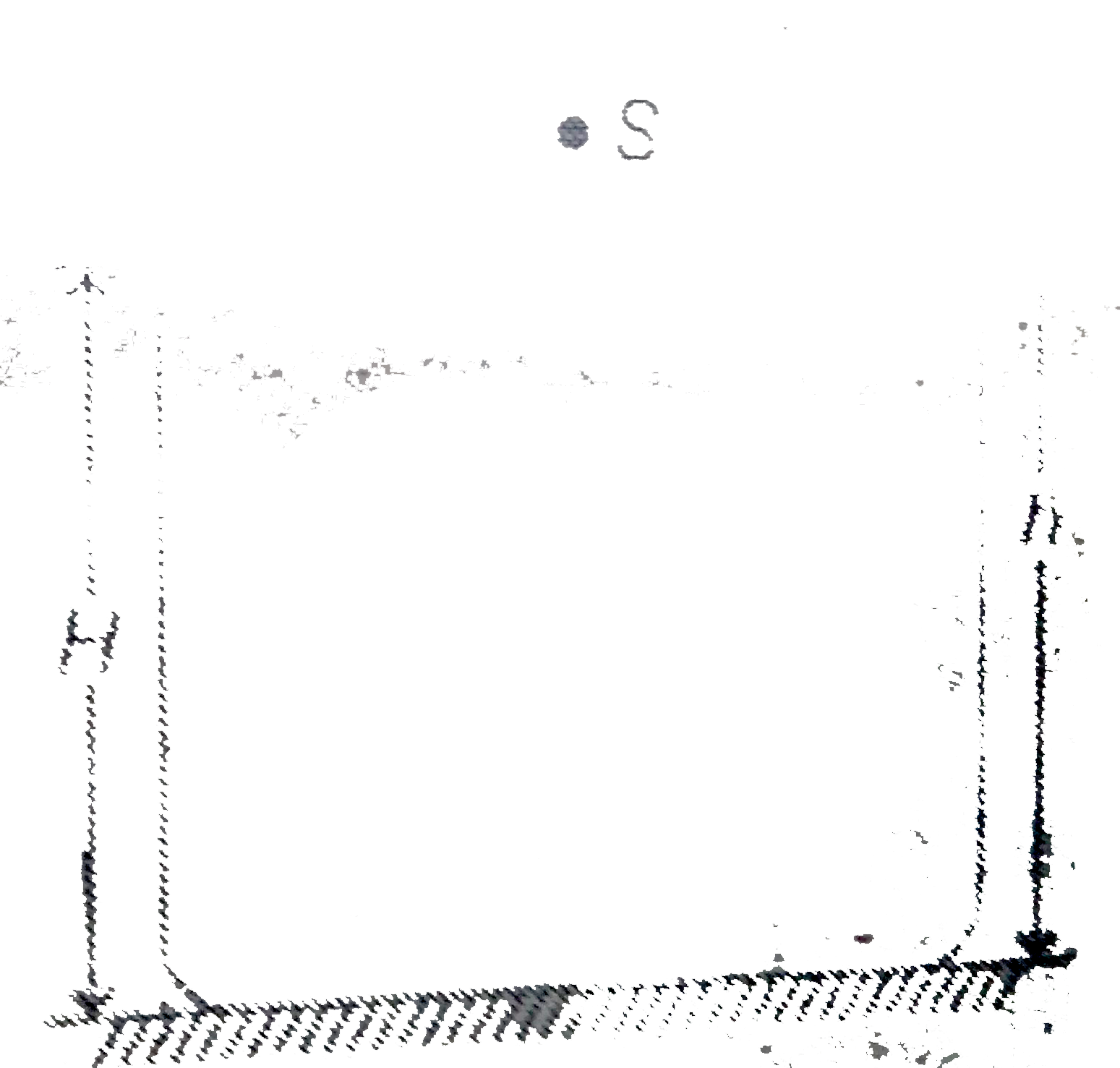 A
A B
B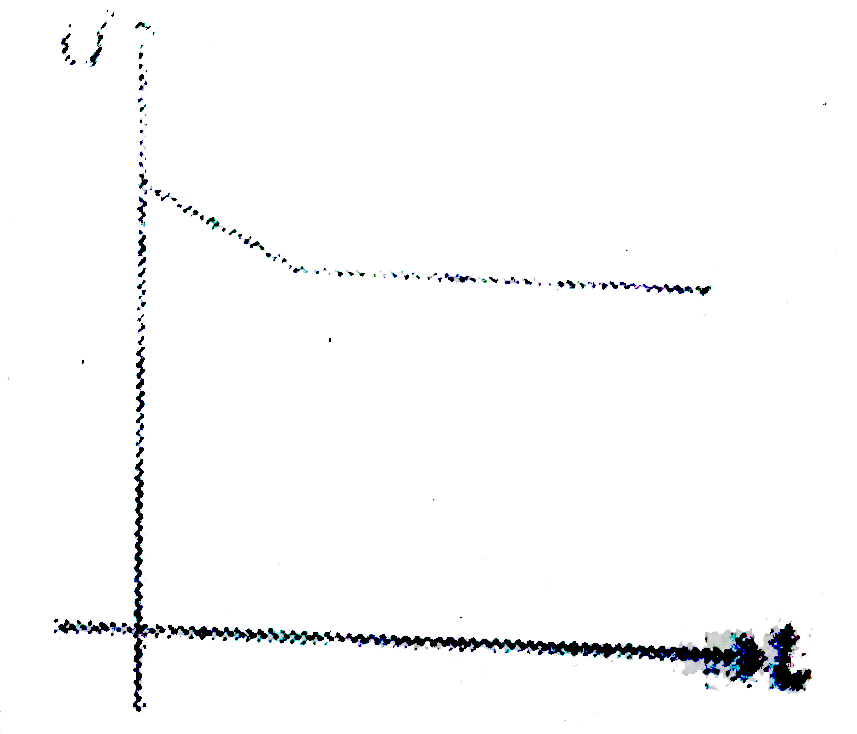 C
C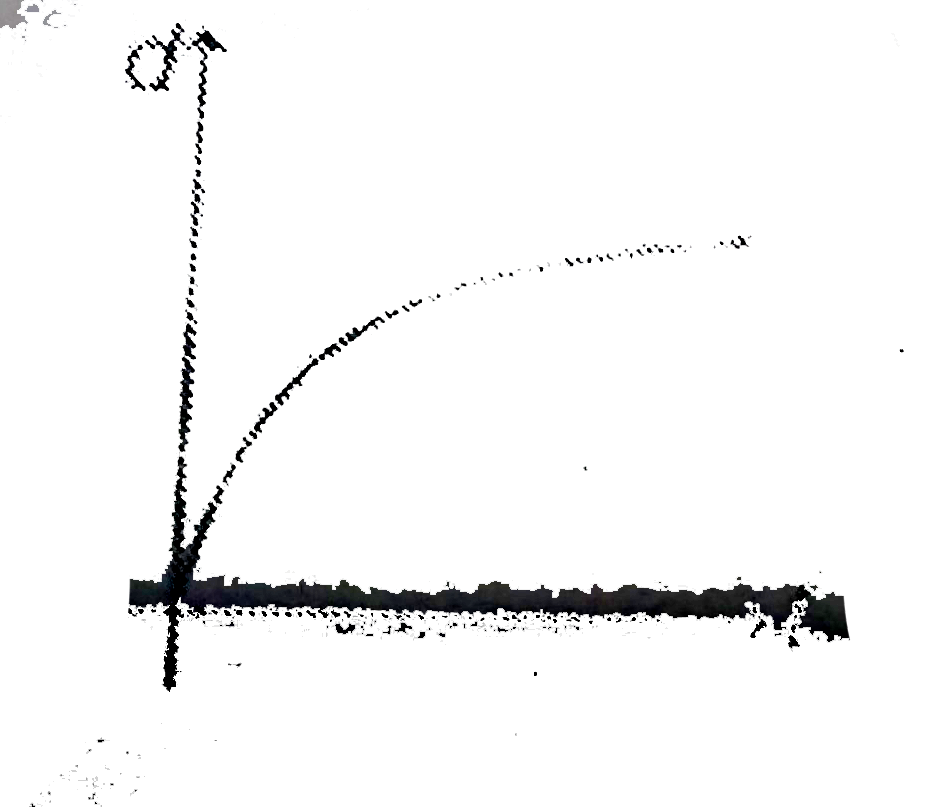 D
D
Water is being poured in a vessel at a constant rate αm2/s. There is a small hole of area a at the bottom of the tank. The maximum level of water in the vessel is proportional to
AαBα2Ca−1Da−2
A conical vessel whose height is 10 meters and the radius of whose base is half that of the height is being filled with a liquid at a uniform rate of 1.5m3/min. Find the rate which the level of the water in the vessel is rising when it is 3m below the top of the vessel.
View SolutionA thin equiconvex glass lens (μg=1.5) is beign placed on the top of a vessel of height h=20cm as shown figure. A luminous point source is beign placed at the bottom of vessel on the principal axis of the lens. When the air is on both the side of the lens the image of luminous source is formed at a distance of 20cm from the lens out side the vessel. When the air inside the vessel is being replaced by a liquid of refractive index μl the image of the same source is being formed at a distance 30cm from the lens outside the vessel. Find the μl.

View SolutionA thin equiconvex glass lens (μg=1.5) is beign placed on the top of a vessel of height h=20cm as shown figure. A luminous point source is beign placed at the bottom of vessel on the principal axis of the lens. When the air is on both the side of the lens the image of luminous source is formed at a distance of 20cm from the lens out side the vessel. When the air inside the vessel is being replaced by a liquid of refractive index μl the image of the same source is being formed at a distance 30cm from the lens outside the vessel. Find the μl.

View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
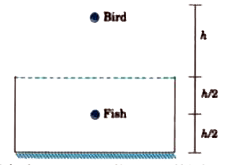
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
View Solution
