A point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
The correct Answer is:C, D
To solve the problem step by step, we will analyze the situation involving the point source of light, the opaque disc, and the refractive index of the liquid.
Step 1: Understand the Setup
- We have a point source of light S at the bottom of a vessel filled with a liquid of refractive index μ=53.
- An opaque disc of radius r=1cm is floating on the surface of the liquid, directly above the source S.
- We need to determine the maximum height h of the liquid such that the source S cannot be seen from above the surface.
Step 2: Identify the Critical Angle
- The critical angle Ic can be calculated using the formula:
μ=1sinIc
- Rearranging gives:
sinIc=1μ=35
- Therefore, the critical angle Ic can be calculated as:
Ic=sin−1(35)
Step 3: Relate the Geometry
- When the light travels from the liquid to the air, the angle of incidence I at the surface of the liquid must be equal to the critical angle Ic for the light to be totally internally reflected.
- The geometry of the situation gives us:
- The radius r of the disc is the horizontal distance from the center of the disc to the edge.
- The height h of the liquid is the vertical distance from the surface of the liquid to the source S.
Step 4: Use Trigonometry
- From the right triangle formed by the height h and radius r, we can use the relationship:
tanIc=rh
- Rearranging gives:
h=rtanIc
Step 5: Calculate tanIc
- We know:
sinIc=35andcosIc=√1−sin2Ic=√1−(35)2=√1625=45
- Therefore, we can find tanIc:
tanIc=sinIccosIc=3545=34
Step 6: Substitute Values
- Now substituting r=1cm and tanIc=34 into the equation for h:
h=1cm34=43cm
Conclusion
- The maximum height of the liquid for which the source cannot be seen from above is:
h=43cm
- We have a point source of light S at the bottom of a vessel filled with a liquid of refractive index μ=53.
- An opaque disc of radius r=1cm is floating on the surface of the liquid, directly above the source S.
- We need to determine the maximum height h of the liquid such that the source S cannot be seen from above the surface.
- The critical angle Ic can be calculated using the formula:
μ=1sinIc
- Rearranging gives:
sinIc=1μ=35
- Therefore, the critical angle Ic can be calculated as:
Ic=sin−1(35)
- When the light travels from the liquid to the air, the angle of incidence I at the surface of the liquid must be equal to the critical angle Ic for the light to be totally internally reflected.
- The geometry of the situation gives us:
- The radius r of the disc is the horizontal distance from the center of the disc to the edge.
- The height h of the liquid is the vertical distance from the surface of the liquid to the source S.
- From the right triangle formed by the height h and radius r, we can use the relationship:
tanIc=rh
- Rearranging gives:
h=rtanIc
- We know:
sinIc=35andcosIc=√1−sin2Ic=√1−(35)2=√1625=45
- Therefore, we can find tanIc:
tanIc=sinIccosIc=3545=34
- Now substituting r=1cm and tanIc=34 into the equation for h:
h=1cm34=43cm
- The maximum height of the liquid for which the source cannot be seen from above is:
h=43cm
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct41videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option3videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective29videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
A small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View Solution
Knowledge Check
- Question 1 - Select One
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2
A point source of light is placed 4 m below the surface of water of refractive index 53. The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut off all light coming out of water is
View SolutionA point source of light is placed at a depth h=0.5 m below the surface of a liquid (μ=54) , Then , the fraction of light energy that escape directly from the liquid surface is
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface area of water is air from water.
View SolutionA point source of light is placed at the bottom of a water lake. If the area of the illuminated circle on the surface is equal to 3 times the square of the depth of the lake. The refractive index of water is
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
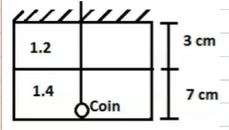 View Solution
View SolutionWhat is the force of surface tension on a light ring of radius r floating on a liquid of surface tension γ ?
View Solution

