Let there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ0(54−rR) upto r = R, and ρ(r)=0 for r >R, where r is the distance from the origin. The electric field at a distance r (r
4πρ0r3ε0(53−rR)
ρ0r4ε0(53−rR)
4ρ0r/(3ε0)(54−rR)
ρ0r3ε0(54−rR)
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
39 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
Similar Questions
Let there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View Solution[" Consider a spherical symmetric "],[" charge distribution with charge "],[" density varying as "],[[rho={[rho_(0)(1-(r)/(R)),r<=R],[0],r>R]]
View Solution
Knowledge Check
Let there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
A(a) ρ0r4ε0(53−rR)B(b) 4πρ0r3ε0(53−rR)C(c) 4ρ0r4ε0(54−rR)D(d) ρ0r3ε0(54−rR)Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
Aρ0r24ε0RBρ0r4ε0RCρ0r4ε0RDρ0r2ε0RA spherical distribution of charge density ρ=ρ0(1−r2/9) exists in the region 0≤r≤2. The dielectric constant of the medium is 2. Find the electric field inside the sphere at a distance r from the centre.
Aρ090ε0[15r−r3]Bρ045ε0[5r−8r3]Cρ05ε0[45r−2r3]Dρ02ε0[3r−4r3]
Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionConsider a spherical symmetric charge distribution with charge density varying as ρ={[ρ0(1−rR),r≤R][0,,r>R]}The electric field at r ,r≤R will be
View SolutionFor spherical charge distribution gives as .
⎧⎨⎩ρ=ρ0(1−r3)whenr≤3mρ=0whenr>3m
( where x is the distance form the centre of spherical charge distribution)
The electric field intensity is maximum for the value of r=_______m.
View SolutionFor spherical charge distribution gives as .
⎧⎨⎩ρ=ρ0(1−r3)whenr≤3mρ=0whenr>3m
( where x is the distance form the centre of spherical charge distribution)
The electric field intensity is maximum for the value of r=_______m.
View SolutionIn a spherical distribution , the charge density varies as ρ(r)=A/r for a<r<b (as shown) where A is constant . A point charge Q lies at the centre of the sphere at r = 0 . The electric filed in the region a<r<b has a constant magnitude for
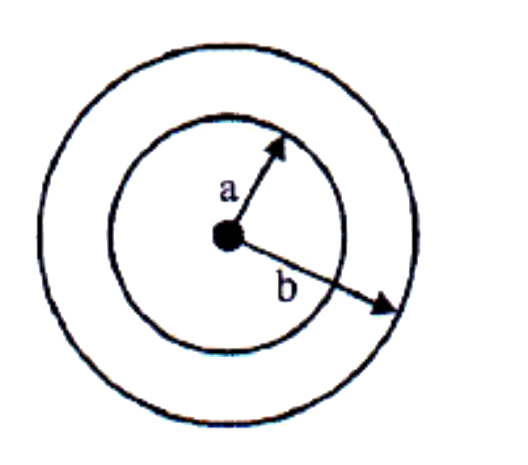
View Solution
