The space between the plates of a parallel plate capacitor is filled with a 'dielectric whose dielectric constant' varies with distance as per the relation :K(x)=K0+λx(λ = a constant). The capacitance C, of this capacitor, would be related to its 'vacuum capacitance C0 as per the relation
C=λd.In(1+k0λd)C0
C=λdIn(1+λd/K0)C0
C=λd.In(1+K0/λd)C0
C=λdIn(1+K−0λd)C0
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
39 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
Similar Questions
Space between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K0+λX,
(λ= constant, K0= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C1 of this capacitor, would be related to its vacuum capacitance C0 per the relation (d = plate separation):
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View Solution
Knowledge Check
A parallel plate capacitor is filled with dielectrics. What is capacitance?
 A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)
A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)Space between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K0+λX,
(λ= constant, K0= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C1 of this capacitor, would be related to its vacuum capacitance C0 per the relation (d = plate separation):AC=λdln(1+K0λd)C0BC=λd.ln(1+K0λd)C0CC=λdln(1+λd/K0)C0DC=λd.ln(1+K0/λd)C0In figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A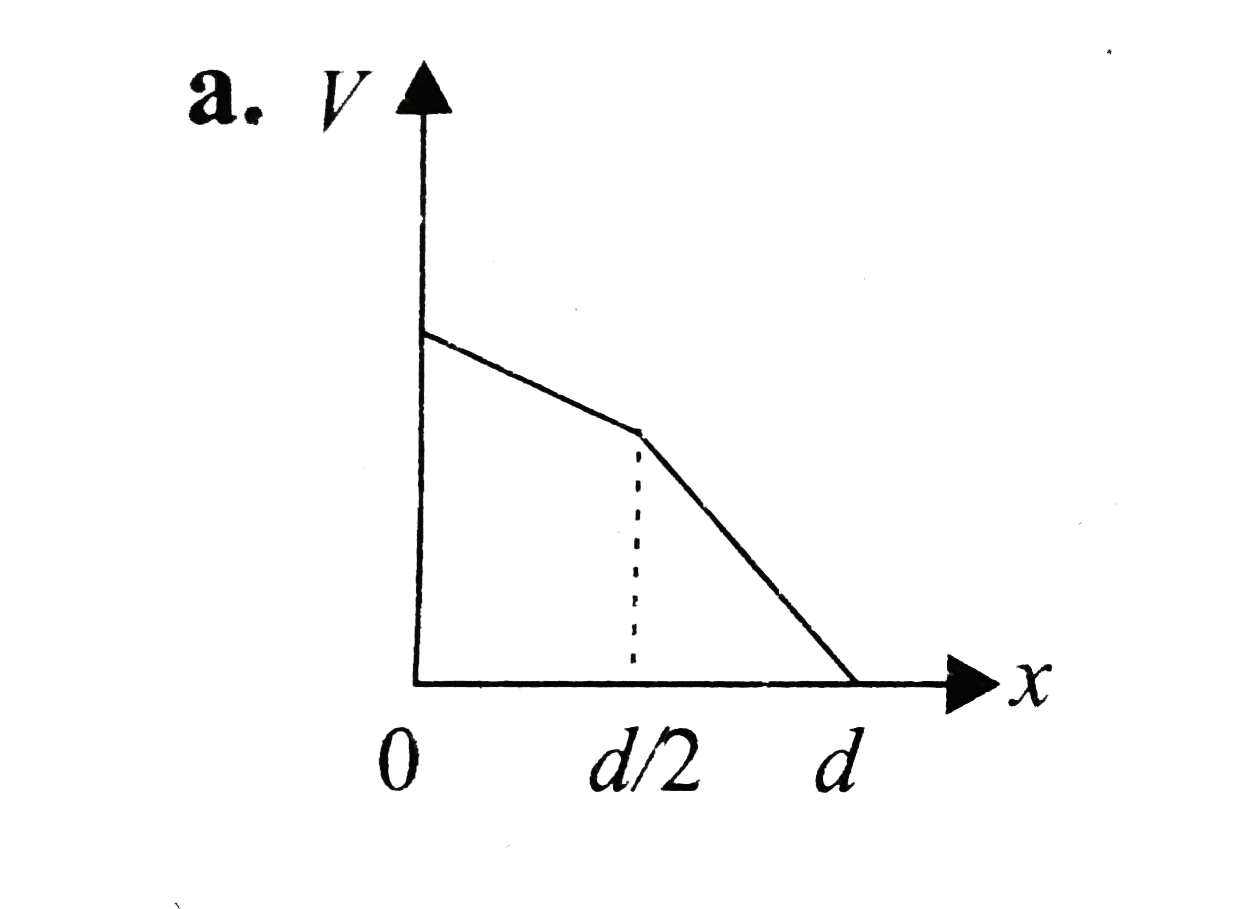 B
B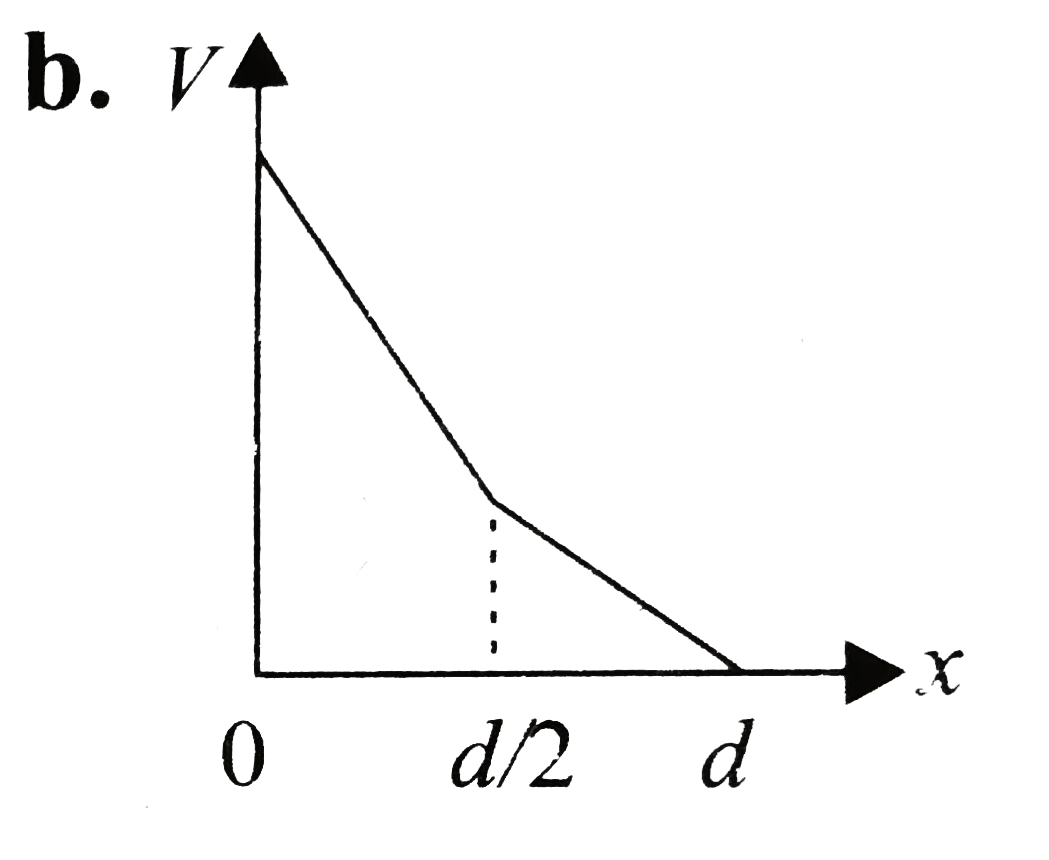 C
C D
D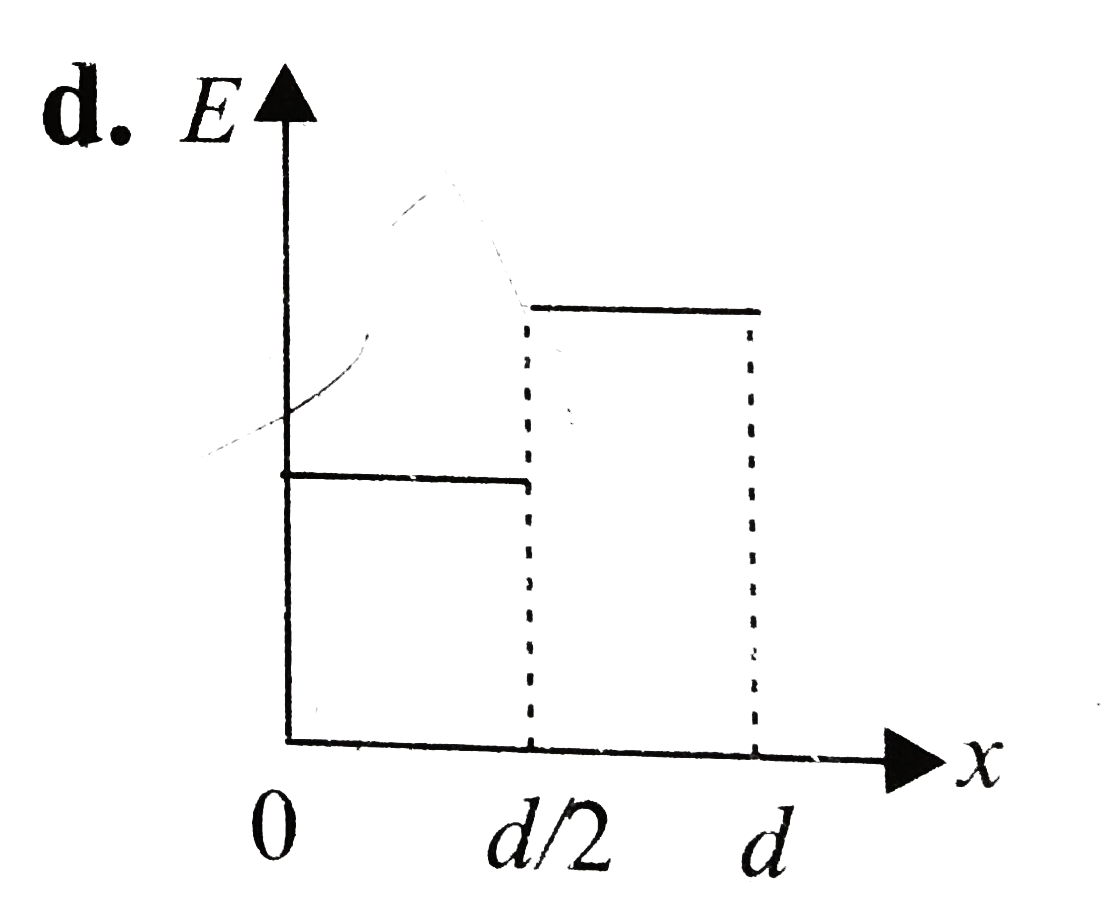
The area of the plates of a parallel plate capacitor is A and the gap between them is d. The gap is filled with a non homogeneneous dielectric whose dielectric constant varies with the distance ‘y’ from one plate as: K=λsec(πy2d), whereλis a dimensionless constant. The capacitance of this capacitor is
View SolutionInside a parallel plate capacitor of width 'd' a di-electric plate with dielectric constant k & width 3d/4 is inserted the new capacitance is C'. Before insertion of dielectric the capacitance was C0. Find relation between C0&C'
View SolutionAn LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionAssertion (A): If the distance between plates of a parallel plate capacitor is halved and the intervening space is filled with a dielectric of dielectric constant 3, the capacitance of capacitor becomes 6 times of its original capacitance.
Reason (R) : The capacitance of a capacitor does not depend on the material of the metal plates.
View SolutionA parallel plate capacitor A is filled with a dielectric whose dielectric constant varies with applied voltage as K = V. An identical capacitor B of capacitance C0 with air as dielectric is connected to voltage source V0=30V and then connected to the first capacitor after disconnecting the voltage source. The charge and voltage on capacitor.
View Solution
