Space between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K0+λX,
(λ= constant, K0= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C1 of this capacitor, would be related to its vacuum capacitance C0 per the relation (d = plate separation):
(a)C=λdln(1+K0λd)C0
(b)C=λd.ln(1+K0λd)C0
(c)C=λdln(1+λd/K0)C0
(d)C=λd.ln(1+K0/λd)C0
The correct Answer is:C
To solve the problem of finding the capacitance C1 of a parallel plate capacitor filled with a dielectric whose dielectric constant varies with distance, we will follow these steps:
Step 1: Understand the Dielectric Constant
The dielectric constant K(x) is given by:
K(x)=K0+λx
where K0 is a constant, λ is a constant, and x is the distance from one of the plates.
Step 2: Write the Expression for Capacitance
The capacitance C of a parallel plate capacitor is given by:
C=K⋅Ad
where K is the dielectric constant, A is the area of the plates, and d is the separation between the plates.
Step 3: Consider a Differential Element
To find the total capacitance when the dielectric constant varies, we consider a small thickness dx of the dielectric. The capacitance dC of this differential element can be expressed as:
dC=K(x)⋅Adx
Substituting K(x):
dC=(K0+λx)⋅Adx
Step 4: Relate Total Capacitance to Differential Capacitance
The total capacitance C1 can be found by integrating the expression for dC from x=0 to x=d:
1C1=∫d0dxdC
This leads to:
1C1=∫d0dx(K0+λx)⋅Adx=1A∫d0dxK0+λx
Step 5: Solve the Integral
The integral can be solved as follows:
∫dxK0+λx=1λln|K0+λx|
Evaluating from 0 to d:
∫d0dxK0+λx=1λ(ln(K0+λd)−ln(K0))=1λln(K0+λdK0)
Step 6: Substitute Back into the Capacitance Formula
Now substituting back into the expression for 1C1:
1C1=1A⋅1λln(K0+λdK0)
Taking the reciprocal gives:
C1=Aλln(K0+λdK0)
Step 7: Relate to Vacuum Capacitance
The vacuum capacitance C0 is given by:
C0=K0⋅Ad
Thus, we can express C1 in terms of C0:
C1=C0⋅λdln(K0+λdK0)
Final Answer
The capacitance C1 of the capacitor filled with the varying dielectric is related to its vacuum capacitance C0 as:
C1=C0⋅λdln(K0+λdK0)
The dielectric constant K(x) is given by:
K(x)=K0+λx
where K0 is a constant, λ is a constant, and x is the distance from one of the plates.
The capacitance C of a parallel plate capacitor is given by:
C=K⋅Ad
where K is the dielectric constant, A is the area of the plates, and d is the separation between the plates.
To find the total capacitance when the dielectric constant varies, we consider a small thickness dx of the dielectric. The capacitance dC of this differential element can be expressed as:
dC=K(x)⋅Adx
Substituting K(x):
dC=(K0+λx)⋅Adx
The total capacitance C1 can be found by integrating the expression for dC from x=0 to x=d:
1C1=∫d0dxdC
This leads to:
1C1=∫d0dx(K0+λx)⋅Adx=1A∫d0dxK0+λx
The integral can be solved as follows:
∫dxK0+λx=1λln|K0+λx|
Evaluating from 0 to d:
∫d0dxK0+λx=1λ(ln(K0+λd)−ln(K0))=1λln(K0+λdK0)
Now substituting back into the expression for 1C1:
1C1=1A⋅1λln(K0+λdK0)
Taking the reciprocal gives:
C1=Aλln(K0+λdK0)
The vacuum capacitance C0 is given by:
C0=K0⋅Ad
Thus, we can express C1 in terms of C0:
C1=C0⋅λdln(K0+λdK0)
The capacitance C1 of the capacitor filled with the varying dielectric is related to its vacuum capacitance C0 as:
C1=C0⋅λdln(K0+λdK0)
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Main (Archive) LEVEL-1
36 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 2
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 1 (MCQs)
60 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View Solution
Knowledge Check
A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A400%B66.6%C33.3%D200%
Figure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as where K and a are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionAn LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionWhen a parallel plate capacitor is filled with wax after separation between plates is doubled, its capacitance becomes twice. What is the dielectric constant of wax?
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
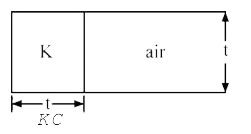
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View Solution
