A stone is projected from the point of a ground in such a direction so as to hit a bird on the top of telegraph post of height h and then attain the maximum height 2h above the ground. If at the instant of projection, the bird were to fly away horizontally with a unifrom speed. Find the ratio between the horizontal velocities of the bird and stone, if the stone still his the bird while ascending.
Let the stone is projected with a velocity u at an angle θ with the horizontal, we have
(2h)=(usinθ)22g or usinθ=2√gh
Suppose t is the time taken by the stone to reach the height h above the ground. Then
h=usinθt−12gt2 (or) gt22−usinθ+h=0
As we have usinθ=2√gh ∴gt22−2√ght+h=0

Solving above equation for t we get
t=2√th±√(2√gh)2−4×g2h2×g2=2√gh±√2ghg
Let t1=√2hg(√2−1) and t2=√2hg(√2+1)
Where t1 and t2 correspond to P and Q in the figure. Suppose v is the horizontal velocity of the bird. Then PQ=vt2
For the motion of stone PQ=ucosθ(t2−t1) ∴vt2=ucosθ(t2−t1)
which gives vucosθ=(t2−t1t2)=√2ghg(√2+1)−(√2−1)√2hg(√2+1)=2√2+1
Similar Questions
A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
View SolutionA stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
View Solution
Knowledge Check
A stone is projected at an angle α to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
A6htanαB6hcotαChtanαDhcotαIf T be the total time of flight and H be the maximum height attained by a stone from the point of projection, then H/T will be ( u=projection velocity and θ=projection angle )
A(1/2)sinθB(1/4)usinθCusinθD2u sinθA stone thrown upwards with speed u attains maximum height h. Ahother stone thrown upwards from the same point with speed 2u attains maximum height H. What is the relation between h and H?
A2h=HB3h=HC4h=HD5h=H
A stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10ms−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
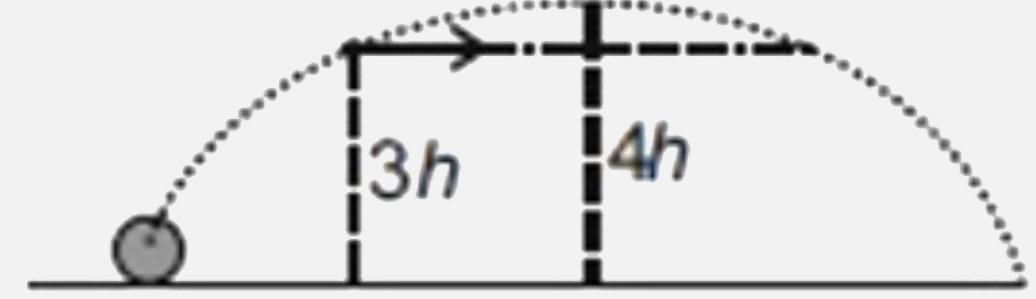
View SolutionA stone is projected at an angle α to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot α from the foot of the lower.
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2sec the angle of elevation of the bird from the same point is 30. Find the speed of flying of the bird.
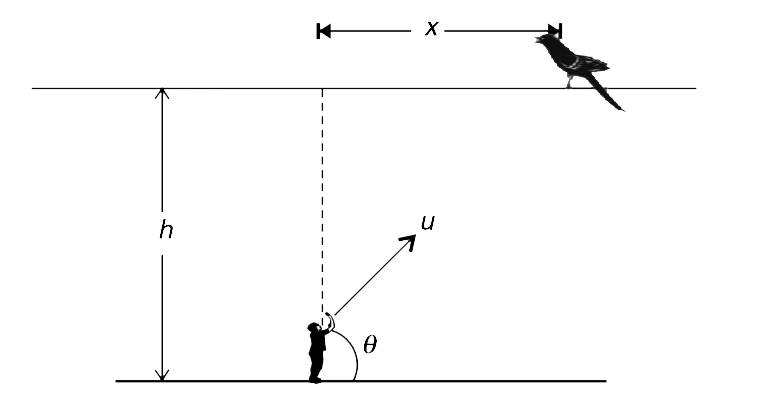
View SolutionA horizontal electric wire is stretched at a height h=10m above the ground. A boy standing on the ground can throw a stone at a speed u=20ms–1. Find the maximum horizontal distance x at which a bird sitting on the wire can be hit by the stone.
View Solution
