A ball starts falling with zero initial velocity on a smooth inclined plane forming an angle $α$ with the horizontal. Having fallen the distnace h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?

Text Solution

Verified by Experts

The situation is shown in fig
Let the ball rebound from point A and return to the plane at point B, moving along the trajectory shown in diagram.

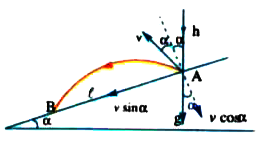
Let $A B = l$
Velocity of rebound at point $A, v = \sqrt{2 g h}$
Velocity component perpendicular to plane $= v cos α$
velocity component along the plane $= v sin α$
Retardation perpendicular to plane $= g cos α$
Acceleration along the plane $= g sin α$
If the ball comes to rest at this highest point after time, t then $(v cos α - g cos α . t) = 0$ or $t = \frac{v}{g}$
Time of fight of the ball $T = 2 t = \frac{2 v}{g}$
Range of the ball along the plane
$l = (v sin α) T + \frac{1}{2} (g sin α) T^{2}$
$= v sin α . \frac{2 v}{g} + \frac{1}{2} . g sin α \frac{4 v^{2}}{g^{2}}$
$= \frac{2 v^{2}}{g} sin α + \frac{2 v^{2}}{g} sin α$
$= 4 \frac{v^{2}}{g} sin α = 4 \frac{(2 g h)}{g} sin α$
$(∴ v = \sqrt{2 g h}) ∴ l = 8 h sin α$

Updated on:21/07/2023