What is the effect on (i) the force constant of the spring (ii) the frequency of oscillations? If the amplitude of oscillations of a loaded spring is doubled.
When amplitude of a loaded spring is doubled then there is no change in the value of force constant of the spring.
(i) Force constant K =Forcedisplacement.
(ii) Time period of a loaded spring T=2π(mk) . It is independent of amplitude of oscillation.
Topper's Solved these Questions
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
33 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-2)
37 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PRACTICE EXERCISE - SPRINGS
16 Videos
Similar Questions
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
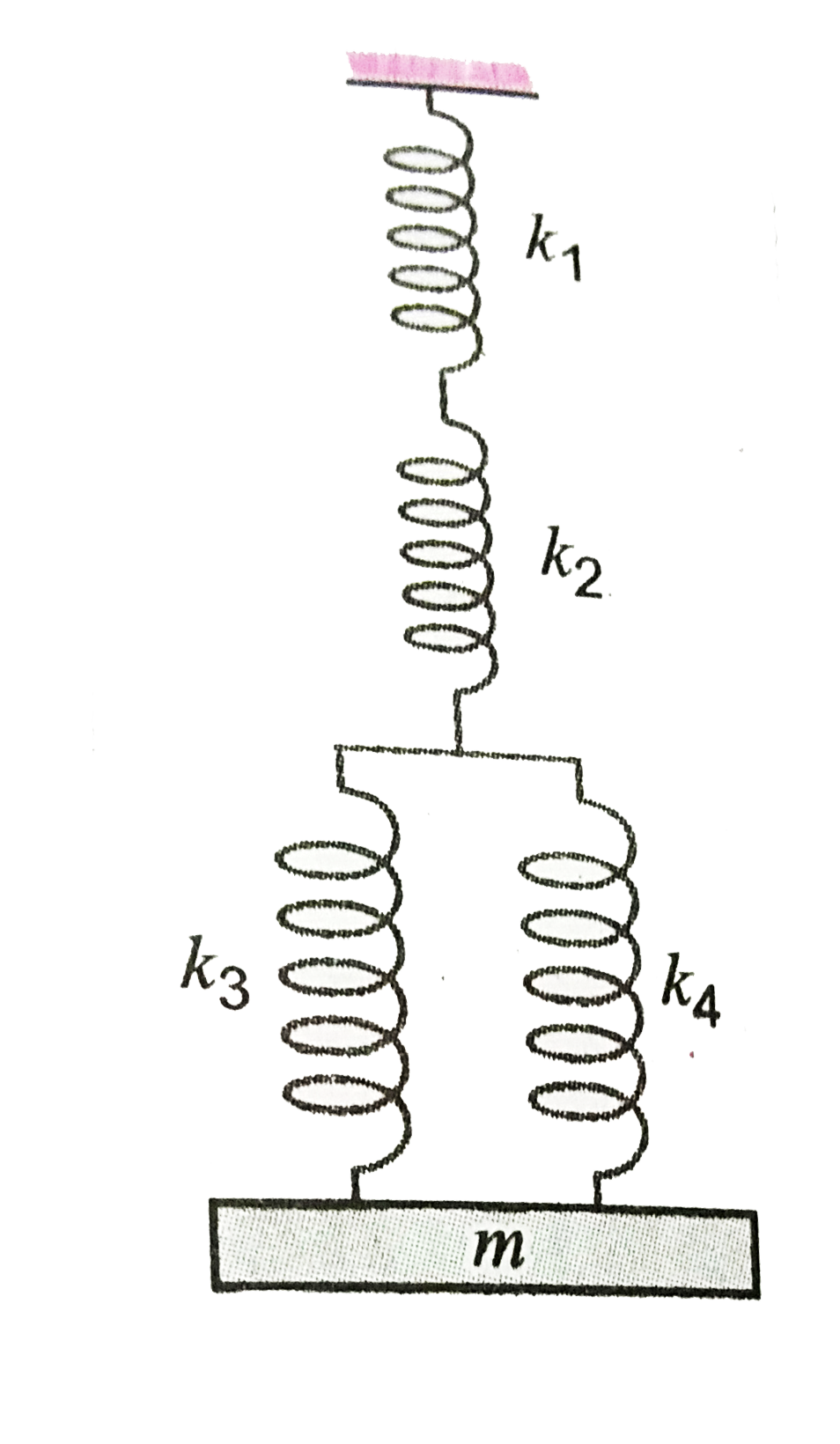
View SolutionA mass of 2 kg is suspended from a vertical spring. An additional force of 2.5 N stretches it by 1 cm. (i) Calculate the force constant. (ii) Calculate the frequecny of oscillations, if the spring is stretched by the given force and then released.
View Solution
Knowledge Check
The frequency of oscillation of the spring shown in the figure will be
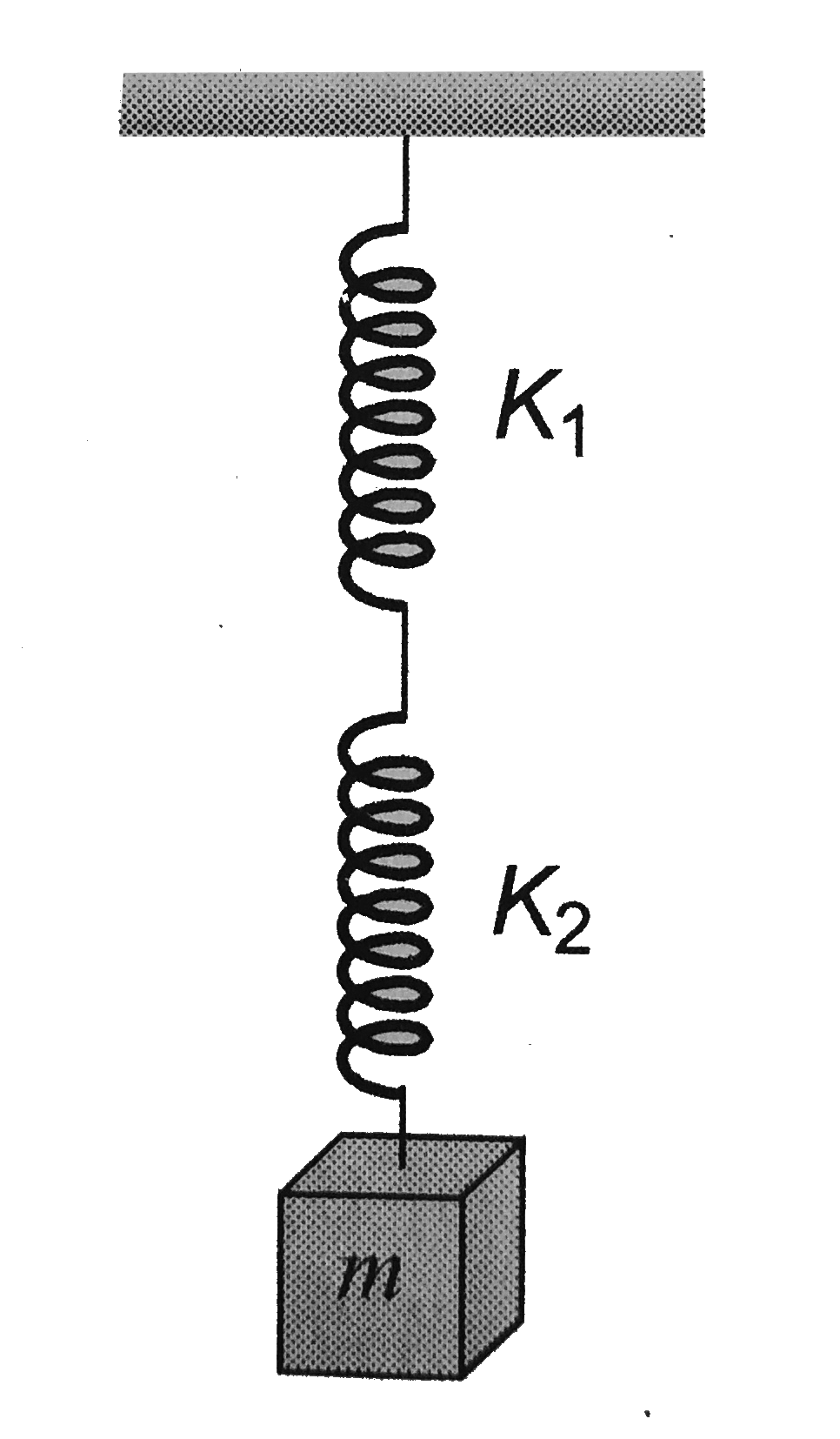 A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2))
A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2))The frequency of oscillation of the springs shown in the figure will be
 A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
Derive an expression for the time -period of the horizontal oscillation of a massless loaded spring.
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
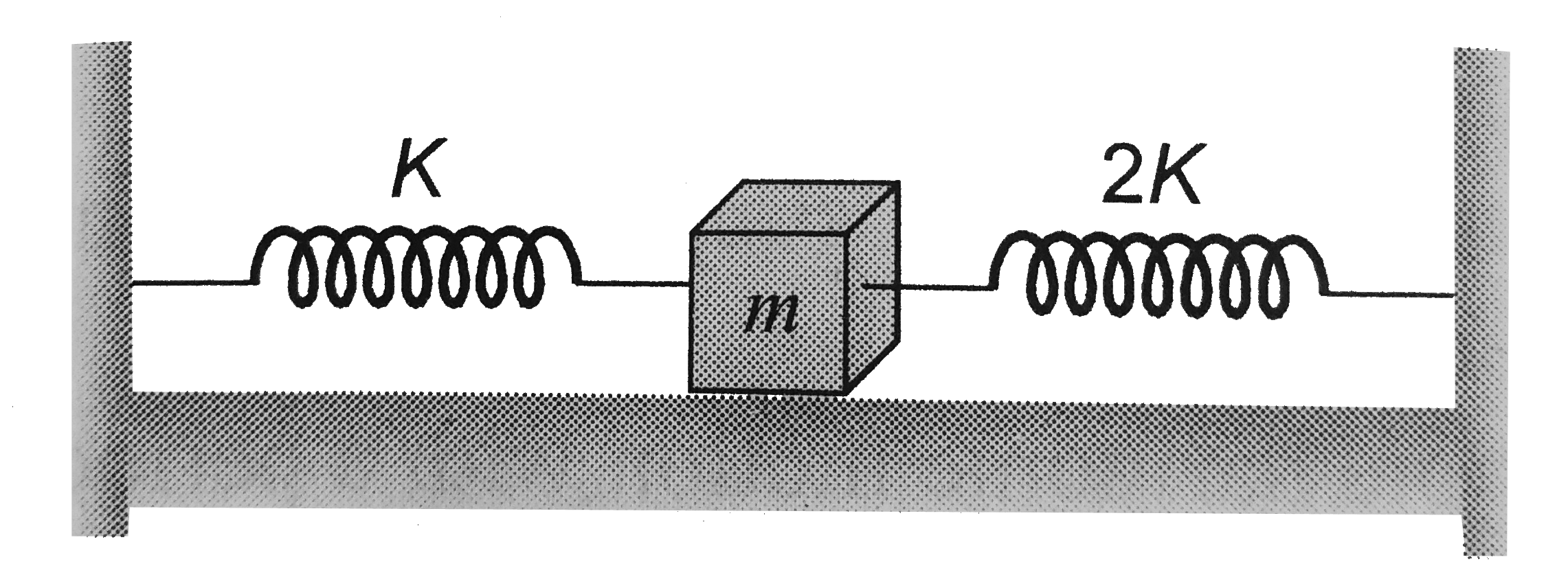
View Solution
