A mass of 2kg attached to a spring of force constant 260 Nm−1 makes 100 oscillation. What is the time taken ?
Mass attached on = 2kg , Force constant k= 260 N/m
∴T=2×3.142×0.0877=0.551 sec
Time for 100 oscillation =100×0.551=55.1 sec.
Topper's Solved these Questions
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
33 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-2)
37 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PRACTICE EXERCISE - SPRINGS
16 Videos
Similar Questions
A block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View Solution
Knowledge Check
A particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
Aπ4Bπ2C2πD8πA mass of 4 kg suspended from a spring of spring constant 800Nm−1 executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum acceleration (in ms−2) of the mass is
A5B15C45D20A mass of 1 kg suspended from a spring whose force constant is 400 Nm−1, executes simple harmonic motion. When the energy of the oscillator is 2J, the maximum acceleration experienced by maas will be
A2ms−2B4ms−2C40ms−2D400ms−2
A 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
View SolutionA 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
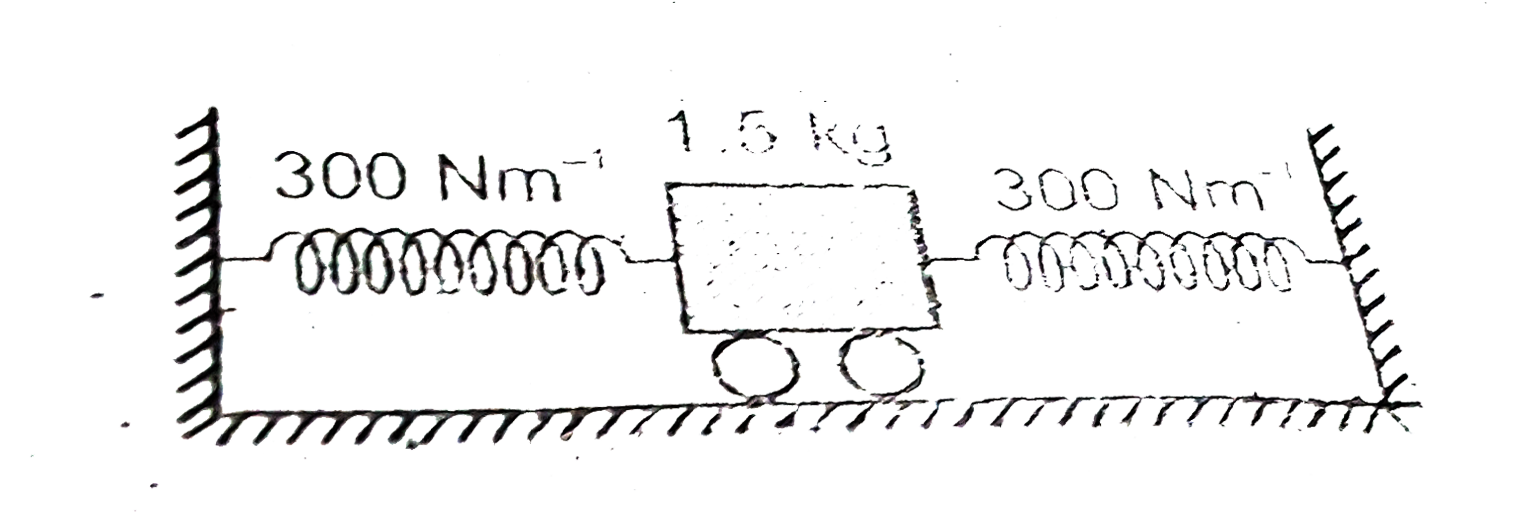
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
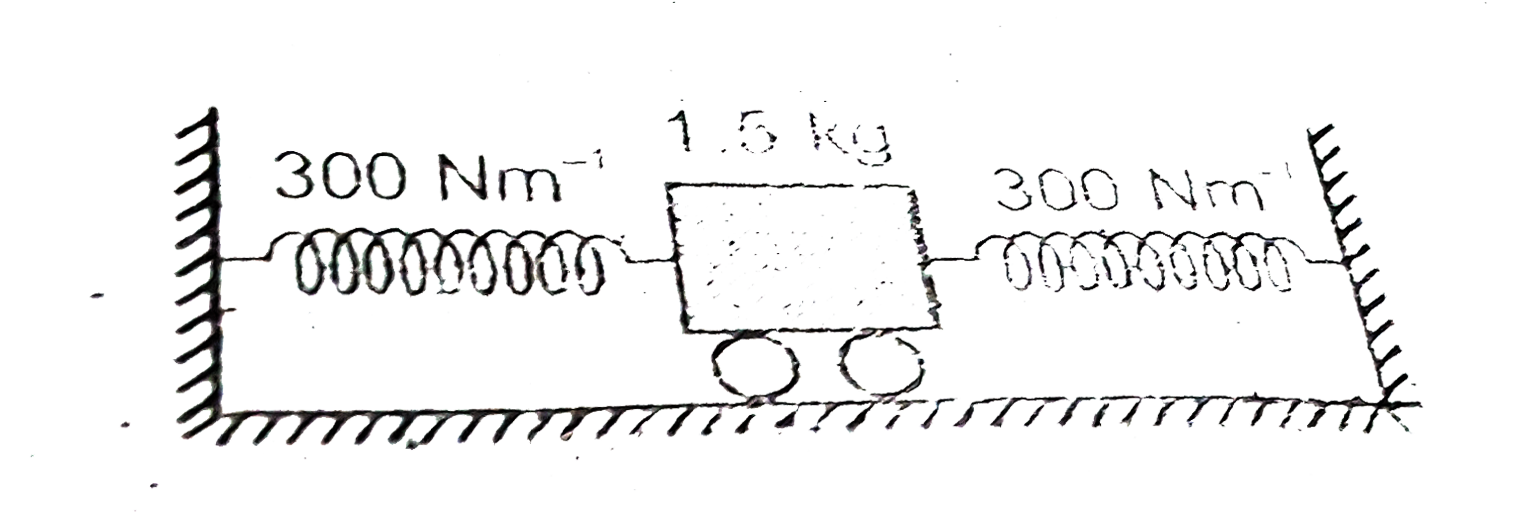
View SolutionA block of mass 0.1 kg is connected to an elastic spring of spring constant 640 Nm−1 and oscillates in a medium of constant 10−2 kg s−1. The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to :
View Solution
