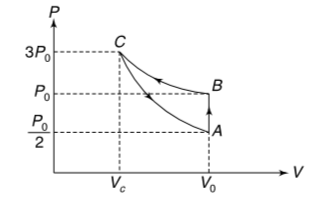
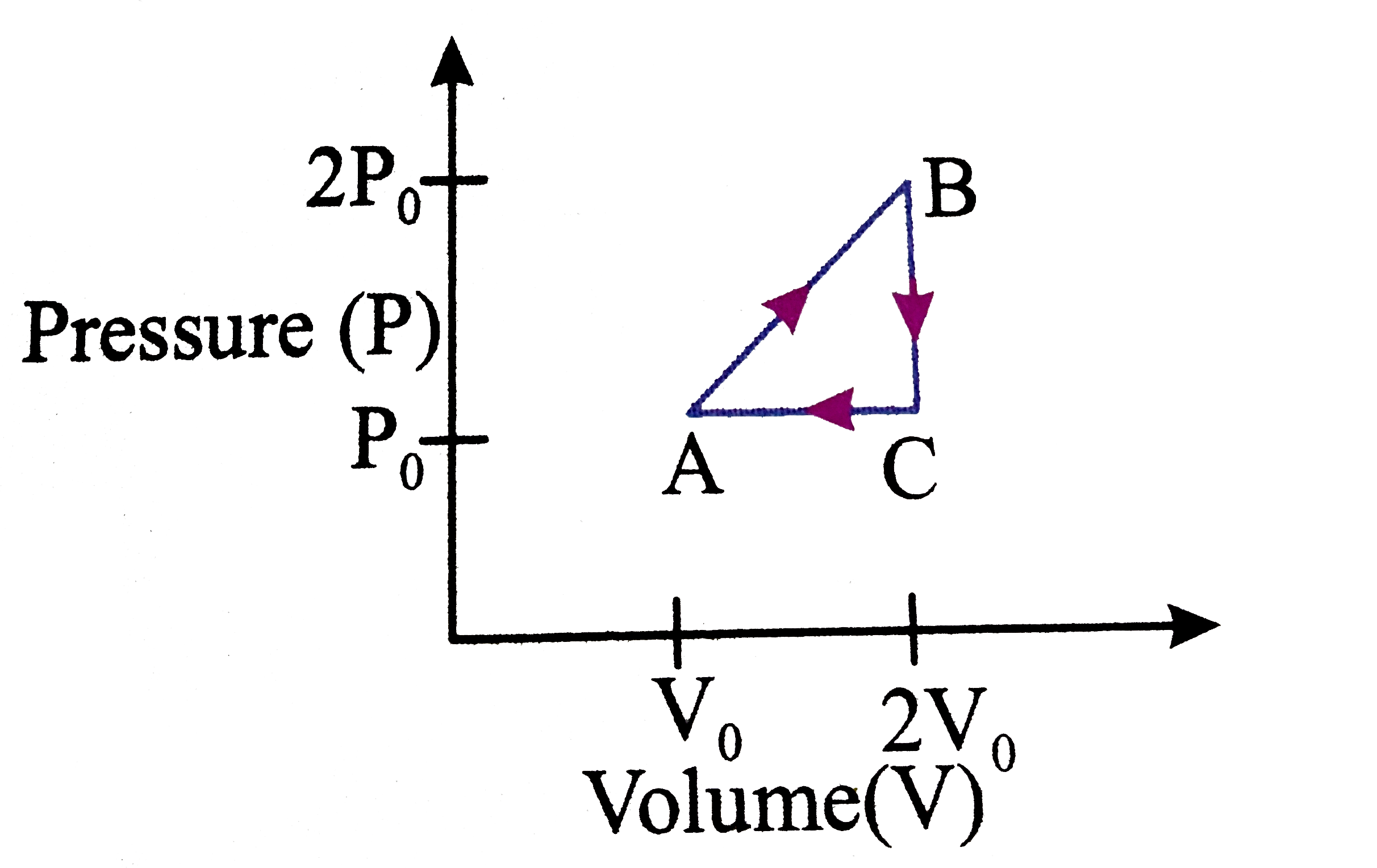Find the efficiency of the thermo-dynamic cycle shown in figure for an ideal diatomic gas.
Let n be the number of moles of the gas and the temperature be T0 in the state A.
Now, work done during the cycle =W=12×(2V0−V0)(2P0−P0)=12P0V0
For the heat (ΔQ1) given during the process A→B, we have ΔQ1−ΔWAB+ΔUAB
ΔWAB= area under the straight line AB=12(P0+2P0)(2V0−V0)=3P0V02
Applying equation of state for the gas in the state A and B.
P0V0T0=(2P0)(2V0)TB=TB=4T0∴UAB=nCv=ΔT=n(5R2)(4T0−T0)=15nRT02=15P0V02
∴ΔQ1=32P0V0+152P0V0=9P0V0
Obviously, the processes B → C and C → A involve the extraction of heat from the gas.
∴ Efficiency (η) of the cycle =work done per cycle Total heat supplied per cyclei.e.,η=12P0V09p0V0=118
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - TEST YOUR SELF
17 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
8 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET ((ADVANCED) INTEGER/SUBJECTIVE TYPE QUESTIONS))
11 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
Knowledge Check
The efficiency of the reversible cycle shown in the figure will be
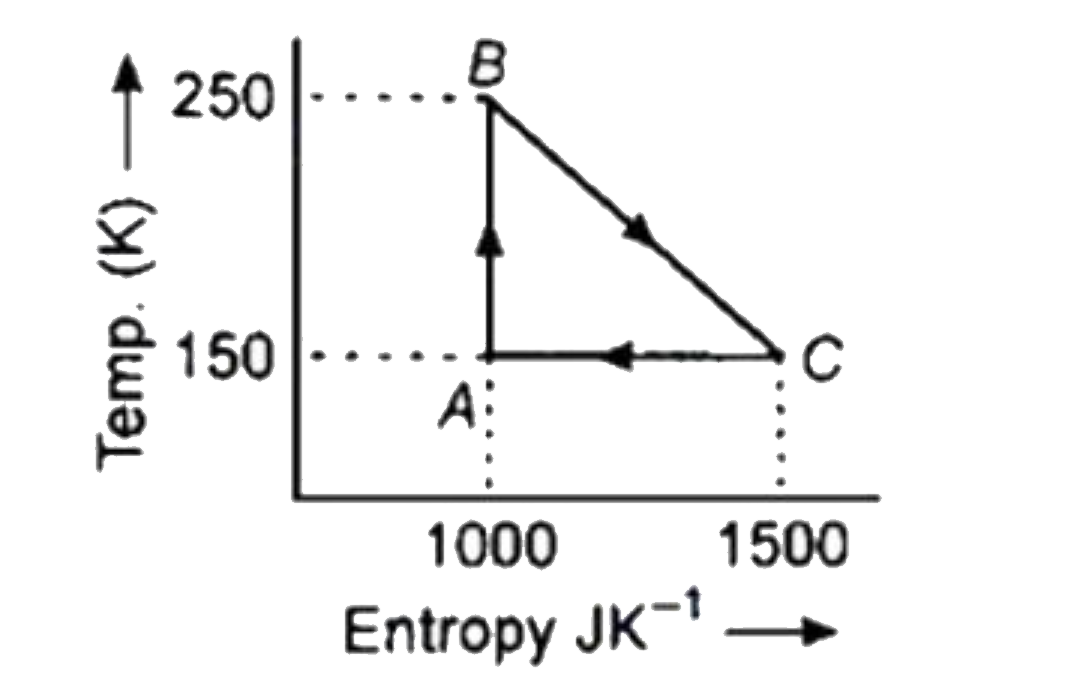 A33.33%B56%C66%D25%
A33.33%B56%C66%D25%The efficiency of the reversible cycle shown in the given figure is
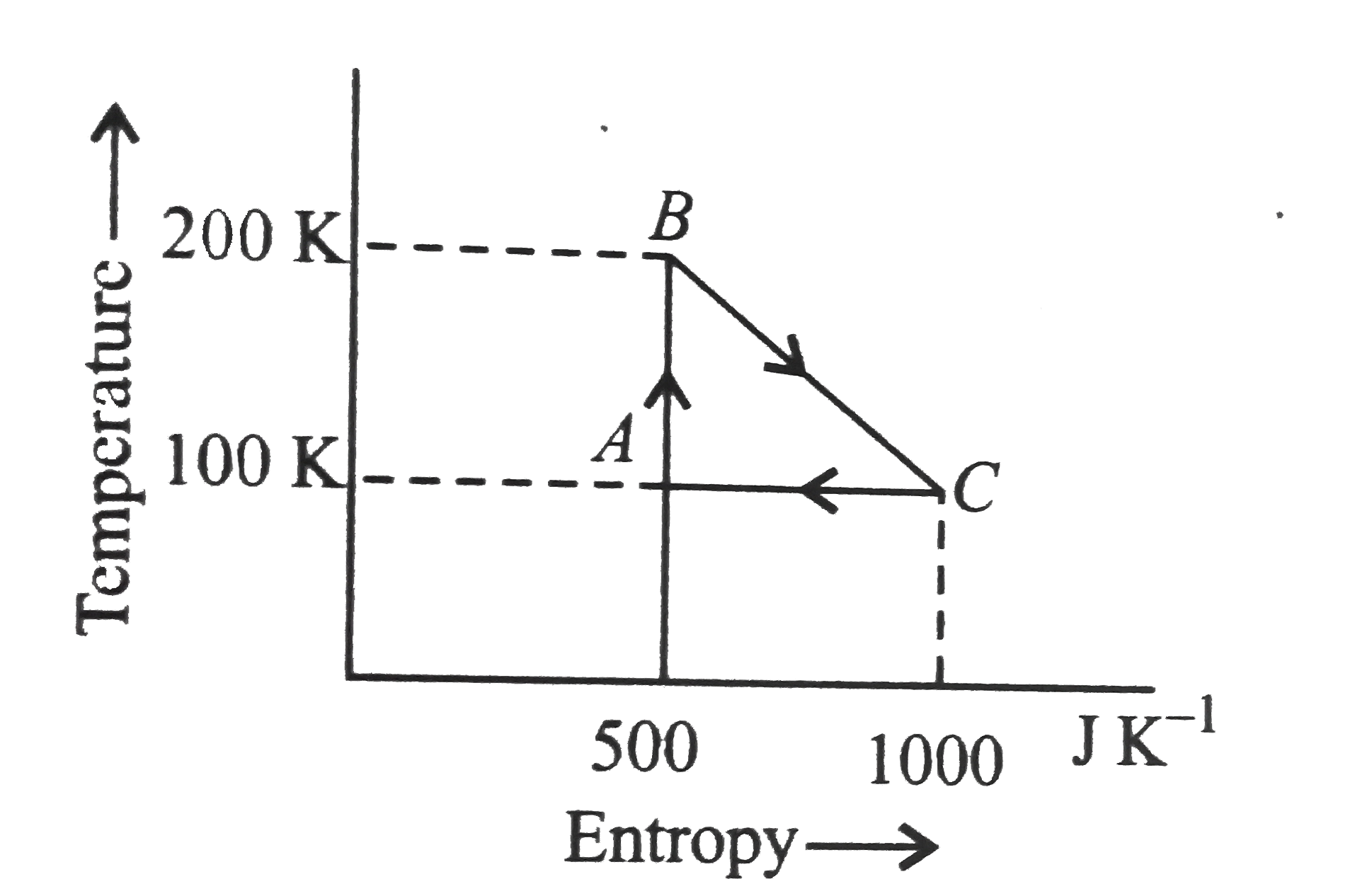 A33.33%B56%C66%D16.7%
A33.33%B56%C66%D16.7%The efficiency of the cycle shown below in the figure ( consisting of one isobar , one adiabatic and one isotherm ( is 50 % the ratio ,x, between the highest and lowest temperature attained in this cycle obeys ( the working substance is an ideal gas )
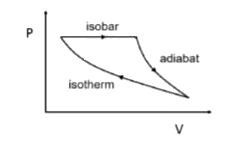 Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1
Ax=ex−1Bx2=ex−1Cx=ex2−1Dx2=ex2−1
The efficiency of the reversible cycle shown in the given figure is

View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.

View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.

View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines if the volume of the ideal gas changes n=10 times within the cycle. The working gas has γ=1.5.
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
View Solution