Indicate the region represented by .
To solve the problem of indicating the region represented by the argument condition π6≤arg(z)≤π4, we can follow these steps:
Step 1: Understand the Argument of a Complex Number
The argument of a complex number z=x+iy is the angle θ formed with the positive real axis in the complex plane. This angle is measured in radians.
Step 2: Identify the Angles
We have two angles given:
- π6 (which is 30 degrees)
- π4 (which is 45 degrees)
Step 3: Draw the Complex Plane
Draw the Cartesian coordinate system with the x-axis (real axis) and the y-axis (imaginary axis).
Step 4: Plot the Angles
- Draw a line from the origin making an angle of π6 with the positive x-axis. This line represents all complex numbers whose argument is π6.
- Draw another line from the origin making an angle of π4 with the positive x-axis. This line represents all complex numbers whose argument is π4.
Step 5: Identify the Region Between the Two Angles
The region we are interested in is the area between these two lines. This region includes all complex numbers whose arguments lie between π6 and π4.
Step 6: Indicate the Region
The required region can be described as:
- It is an infinite wedge starting from the origin and extending outwards, bounded by the two lines representing π6 and π4.
Summary of the Solution
The region represented by π6≤arg(z)≤π4 is the area between the lines corresponding to these angles in the complex plane.
---
The argument of a complex number z=x+iy is the angle θ formed with the positive real axis in the complex plane. This angle is measured in radians.
We have two angles given:
- π6 (which is 30 degrees)
- π4 (which is 45 degrees)
Draw the Cartesian coordinate system with the x-axis (real axis) and the y-axis (imaginary axis).
- Draw a line from the origin making an angle of π6 with the positive x-axis. This line represents all complex numbers whose argument is π6.
- Draw another line from the origin making an angle of π4 with the positive x-axis. This line represents all complex numbers whose argument is π4.
The region we are interested in is the area between these two lines. This region includes all complex numbers whose arguments lie between π6 and π4.
The required region can be described as:
- It is an infinite wedge starting from the origin and extending outwards, bounded by the two lines representing π6 and π4.
The region represented by π6≤arg(z)≤π4 is the area between the lines corresponding to these angles in the complex plane.
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - A DAS GUPTACHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
224 Videos
- Circular Functions, Identities BOOK - A DAS GUPTACHAPTER - Circular Functions, Identities EXERCISE - Exercise
300 Videos
- Continuity, Differentiability and Graph of FunctionBOOK - A DAS GUPTACHAPTER - Continuity, Differentiability and Graph of FunctionEXERCISE - Exercise
38 Videos
Similar Questions
Knowledge Check
The region represented by 2x+y≥6 is
AboundedBunboundedCdoes not existDNone of theseThe shaded region is represented by the inequality:
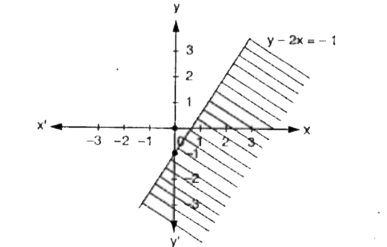 Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1The shaded region is represented by the inequation:
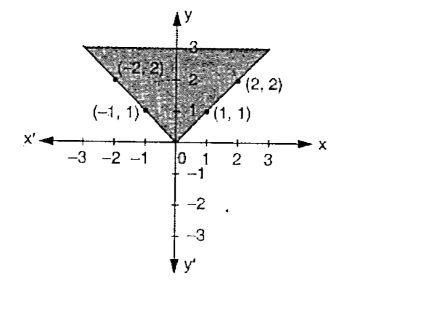 Ay≥xBy≥−xCy≥|x|Dy≤|x|
Ay≥xBy≥−xCy≥|x|Dy≤|x|
The region represented by 2x+y≥6 is
View SolutionFeasible region is represented by
View SolutionPlot the region represented by π3≤arg(z+1z−1)≤2π3 in the Argand plane.
View SolutionConstruct the region represented by the inequations x+y≥4and3x+2y≤6.
View SolutionIndicate the region in the Argand plane respresented by |z+1|2+|z−1|2=4 .
View Solution