Plot the region represented by π3≤arg(z+1z−1)≤2π3 in the Argand plane.
Step by step video & image solution for Plot the region represented by pi/3lt=a r g((z+1)/(z-1))lt=(2pi)/3 in the Argand plane. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Plot the region represented by π3≤arg(z+1z−1)≤2π3 in the Argand plane.
View SolutionWhat is the region represented by the inequality 3<|z−2−3i|<4 in the Argand plane
View SolutionThe region represented by RE(z)≤2,Im(z)≤2 and π8≤arg(z)≤3π8 lies in
View SolutionThe region represented by the inequality 2<|z+i|≤3 is . . . .
View SolutionThe area bounded by the curves argz=π3andargz=2π3andarg(z−2−2i√3)=π in the argand plane is (in sq. units)
View SolutionGiven z1=1+2i. Determine the region in the complex plane represented by 1<|z−z1|≤3. Represent it with the help of an Argand diagram
View SolutionIf z4=(z−1)4 then the roots are represented in the Argand plane by the points that are
View SolutionFind the area bounded by |argz|≤π/4 and |z−1|<|z−3|.
View SolutionThe shaded region, where P=(−1,0),Q=(−1+√2,√2)R=(−1+√2,−√2),S=(1,0) is represented by Figure
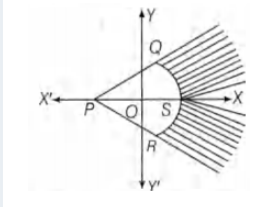
|z+1|>2,∣arg(z+1)<π4
|z+1|<2,∣arg(z+1)<π2
|z+1|>2,∣arg(z+1)>π4
|z+1|<2,∣arg(z+1)>π2
View SolutionGiven that the complex numbers which satisfy the equation ∣∣zz3∣∣+∣∣zz3∣∣=350 form a rectangle in the Argand plane with the length of its diagonal having an integral number of units, then area of rectangle is 48 sq. units if z1,z2,z3,z4 are vertices of rectangle, then z1+z2+z3+z4=0 rectangle is symmetrical about the real axis arg(z1−z3)=π4or3π4
View Solution
