Find the centroid of a triangle, the mid-point of whose sides are D(1, 2, -3), E(3, 0, 1) and F(-1, 1, -4).Solution in Gujrati
The correct Answer is:(1, 1, -2)
Step by step video, text & image solution for Find the centroid of a triangle, the mid-point of whose sides are D(1, 2, -3), E(3, 0, 1) and F(-1, 1, -4). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - SOLUTION OF NCERT EXEMPLAR PROBLEMS (LONG ANSWER TYPE QUESTIONS)4videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - SOLUTION OF NCERT EXEMPLAR PROBLEMS (OBJECTIVE TYPE QUESTIONS)13videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - KUMAR PRAKASHANCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK13videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - KUMAR PRAKASHANCHAPTER - CONIC SECTIONSEXERCISE - QUESTION OF MODULE9videos
CONIC SECTIONS
- BOOK - KUMAR PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Textbook Illustrations for practice work35videos
LIMITS AND DERIVATIVES
Similar Questions
Show that the three points A(2, 3, 4), B(-1, 2, -3) and C(-4, 1, -10) are collinear and find the ratio in which C divides ¯¯¯¯¯¯AB.
05:18View SolutionThe distance of point P(3, 4, 5) from the YZ-plane is ____ .
05:18View SolutionIn Figure, if P is (2, 4, 5), find the coordinates of F.
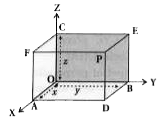 02:57View Solution
02:57View SolutionObtain the equation oc circle with centre (3,-2) and radius √5 unit.
06:32View SolutionFind the limits:
limx→1[x3−x2+1]03:11View SolutionThe points (1,-1),(2,-1) and (4,-3) are the mid-points of the sides of a triangle. Then its centroid is
03:07View SolutionThe points (1,-1),(2,-1) and (4,-3) are the mid-points of the sides of a triangle. Then its centroid is
03:26View SolutionIf the points (1,-1), (2,-1) and (4,-3) are the mid points of the sides of a triangle then write the coordinates of its centroid.
View SolutionIf mid-points of the sides of a triangle are (1, 2, -3), (3, 0, 1) and (-1, 1, -4). Find its vertices.
01:47View SolutionIt the mid-points of the sides of triangle are (1, 2, -3),
(3, 0, 1) and (2, -2, 5), then the centroid is06:32View SolutionIf (32,0),(32,6) and (−1,6) are mid-points of the sides of a triangle, then find
Centroid of the triangle10:39View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
03:16View SolutionIf (1,0,3),(2,1,5),(−2,3,6) are the mid-points of the sides of a tringle, then the centroid of the triangle is
04:36View SolutionIf the coordinates of the mid-points of the sides of a triangle are (1, 1) , (2, -3) and (3, 4). Find the coordinates of the centroid.
03:26View SolutionIf the points (1,-1), (2,-1) and (4,-3) are the mid points of the sides of a triangle then write the coordinates of its centroid.
07:42View Solution

