समीकरण निकाय x+y=2π3,cosx+cosy=32 जहाँ x तथा y वास्तविक है, का हल समुच्चय …………. है।
The correct Answer is:ϕ
Step by step video, text & image solution for समीकरण निकाय x+y=(2pi)/(3), cosx+cosy=(3)/(2) जहाँ x तथा y वास्तविक है, का हल समुच्चय …………. है। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमीतीय समीकरणBOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (स्तम्भ सुमेलन)
1 Videos
- त्रिकोणमीतीय समीकरणBOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (कथन एवं कारण)
2 Videos
- त्रिकोणमीतीय समीकरणBOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (सत्य/असत्य)
2 Videos
- त्रिकोणमितीय अनुपात एवं सर्वसमिकायें BOOK - ALLEN HINDICHAPTER - त्रिकोणमितीय अनुपात एवं सर्वसमिकायें EXERCISE - EXERCISE - 04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
11 Videos
- त्रिभुज के हल BOOK - ALLEN HINDICHAPTER - त्रिभुज के हल EXERCISE - DO YOURSELF 10
1 Videos
Similar Questions
निम्न प्रश्न में दो स्तम्भ में वक्त्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है। स्तम्भ-I (Column-I) के वक्त्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्त्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्त्तव्य स्तम्भ -II (Column-II) के एक वक्त्तव्य से सही सुमेल करता है।
बायीं तरफ समीकरण, अन्त्राल के साथ दी गई है तथा दायीं तरफ हलों की संख्या दी गई है तब सुमेलित कीजिए
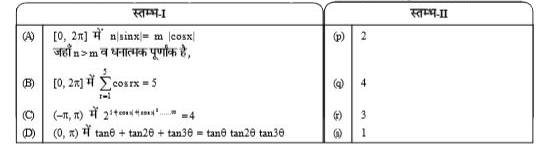
View Solutionकथन-I : θ≠(2n+1)π या (2n+1)π/2,n∈I के किसी वास्तविक मान के लिए व्यंजक y=cos2θ−1cos2θ+cosθ का मान y≤0 या y≥2
क्योंकि
कथन-II : θ के सभी वास्तविक मानों के लिए secθ∈(−∞,−1]∪[1,∞)
View Solution[0,π2] में सभी θ के लिए cos(sinθ)>sin(cosθ) है।
View Solutionसिद्ध कीजिए:
न्यूनकोण त्रिभुज ABC में ΣsecA तथा Σtan2A का न्यूनतम मान क्रमश: 6 तथा 9 है।
View Solutionएक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र (परिकेन्द्र) सम्पाती होते हैं |
View Solutionसमीकरण y=sinx तथा y=sin2x का हल है जब 0∘≤x≤90∘-
View Solutionसमीकरण e−x+ydydx=1 का हल है -
View Solutionसमीकरण dydx=exy+y का हल है -
View Solutionसमीकरण (x2+1)dydx=1 का हल है -
View Solutionλ के किस मान के लिए निम्न समीकरण के निकाय
2x−y−2z=2,x−2y+z=−4,x+y+λz=4 का कोई हल नहीं है
View Solutionसमीकरण dydx+1y+y=0 का हल है -
View Solutionअवकल समीकरण xdydx−y√x2−y2=10x2 का हल है-
View Solutionc∈R का अधिकतम मान, जिसके लिए रेखिक समीकरण निकाय x−cy−cz=0,cx−y+cz=0,cx+cy−z=0 का एक अत्युच्च हल है, है
View Solutionमाना y=y(x), अवकल समीकरण (x2+1)2dydx+2x(x2+1)y=1 का हल है, जबकि y(0) = 0 है। यदि √ay(1)=π32 है तो 'α' का मान है
View Solutionअवकल समीकरण xdydx+2y=x2(x≠0) का हल जिसके लिए y(1) = 1 है, है
View Solutionयदि अवकल समीकरण dydx+(2x+1x)y=e−2x,x>0 का हल y(x) है , जहाँ y(1)=12e−2, तो
View Solution
