A cylinder block of length 0.4m and area of cross - section is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the block is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300 K . If the thermal conductivity of teh material of the cylinder is 10 Watt/mK and the specific heat of the material of the disc is 600J/kg - k, how long with it take for the temperature of the disc to increse to 350 K ? Assume , for purpose of calculation , the thermal conducity of the disc to be very high and the system to be themally insulated except for the upper face of the cylinder .
Fundamental quation of heat conduction is steady state is .
In this cause the temperature of upper face of cylinder is , while the temperature of lower face of cylinder is changing . Therefore ,we shall use equation (1) in the form
where T is any intermediate temperature of lower face of cylinder , dQ is heat absorbed by disc in time dt dQ = mc , dT , Here m = mass of disc 0.4 kg , c = specific heat of disc = 600 j/kg - K.
Integrating
substituting given values , we get sec = 2 min . 46 sec .
Topper's Solved these Questions
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - TEST YOUR SELF
6 Videos
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
28 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
- TRANSMISSION OF HEATBOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)
3 Videos
Similar Questions
Why copper is used at the bottom of cooking untensils and why they are provided with wooden handles ?
View SolutionWhat is the dimensional formula and what is SI unit of coeffcient of thermal conductivity ?
View SolutionIf a temperature scale defines the freezing point of water as 100∘C and the boiling as 0∘ what temperature on the scale corresponds to 25∘ C ?
View SolutionA body cools in 7 minute from 600C to 400C. Temperature after the next 7 minutes is 7x. Find .x.. (The temperature (in degree) of surrounding is 100C).
View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04 m^2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10 "watt"// m-K and the specific heat of the material of the disc is 600J//kg-K , how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionIf l is the length, A is the area of cross-section and K the thermal conductivity, then the thermal resistance of the block is given by
View Solution_S01_005_Q01.png)
Find out the elongation in block. If mass area of cross-section and young modulus of block are m, A and y respectively.
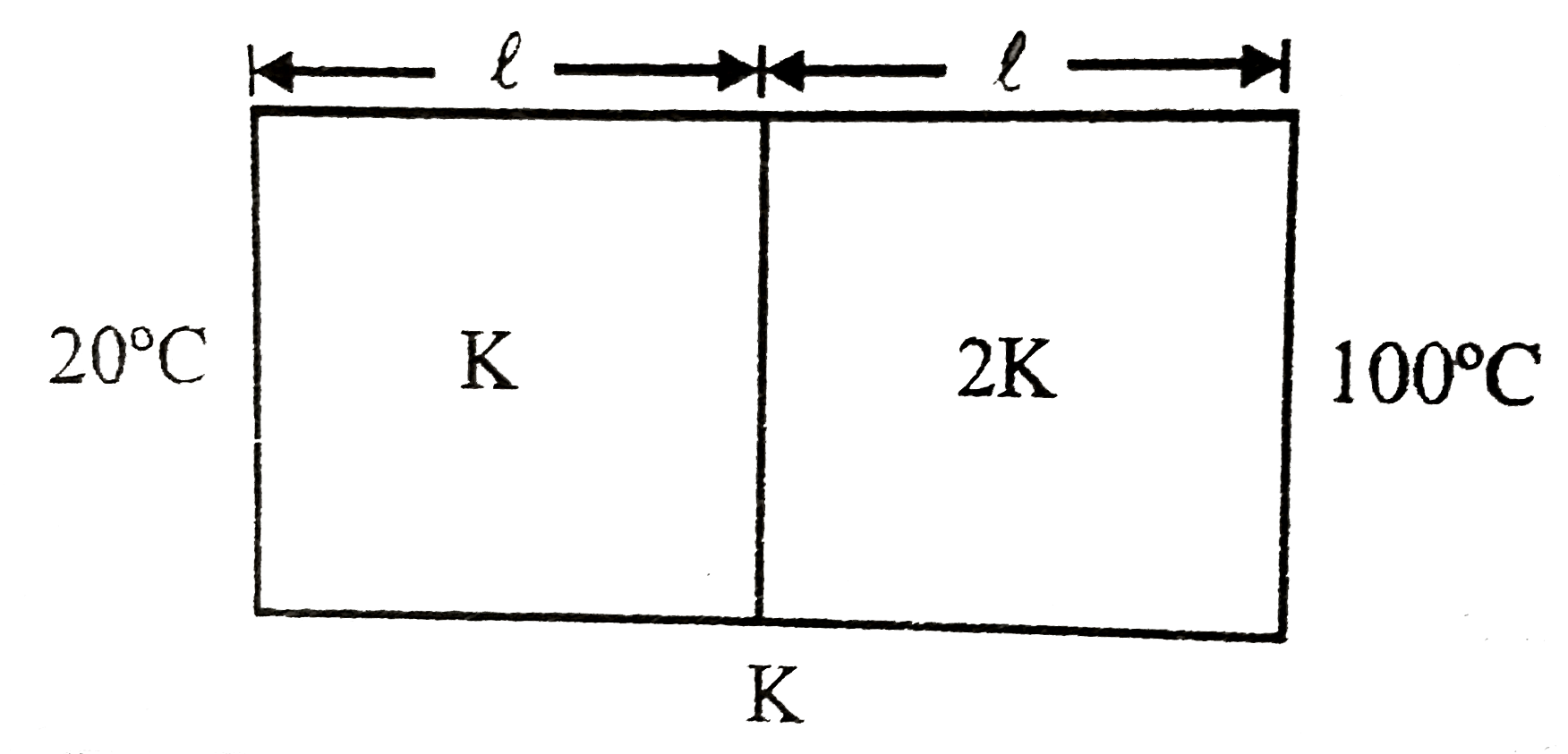
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
View SolutionA disc of radius is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block is mu_(K)= 0.4 , then find the maximum distance from axis where the block can be placed without slidding:
View SolutionWhat is the relationship between length of a conductor and its resistance ? Write the experimental procedure to verify that relationship.
View SolutionWhat is the relationship between length of a conductor and its resistance ? Write the experimental procedure to verify that relationship.
View SolutionA thin metal disc of mass 0.5 kg and cross sectional area 0.05m2 is placed coaxially with a cylindrical block of height 0.5 m and same cross sectional area. The top face of the cylindrical block is maintained at a constant temperature of 300 K. If the initial temperature of the metal disc is 200 K, how long will it take for its temperature to raise to 250 K? The thermal conductivity of cylinder's material is 10Wm−1K−1 and specific heat capacity of disc's metal is 600Jkg−1K−1
Note: Consider that the thermal conductivity of disc is very high and the system is thermally insulated except the top face of cylinder.
View SolutionT উষ্ণতায় একটি ব্রোঞ্জ পিনের প্রস্থচ্ছেদের ক্ষেত্রফল স্টিলের ব্লকে একটি গর্তের প্রস্থচ্ছেদ অপেক্ষা সামান্য বেশি হওয়ায় পিনটিকে ওই গর্তে ঢোকানো যায় না। ন্যূনতম উষ্ণতার পরিবর্তনে যেক্ষেত্রে পিনটিকে ব্লকে ঢোকানো যাবে তা হল
View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4kg and of the same cross section. The upper face of the cylinder is maintained at constant temperature of 400 K and the initial temperature of the disk is 300K. If the thermal conductivity of the material of the cylinder is 1 wm−1K−1 and the specific heat of the material of the disk is 600 j\kg -K, how long will it take for the temperature of the disc to increase to 350 K. (Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder)
View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04m^(2) is placed coaxially on a thin metal, disc of mass 0.4 kg and same cross-section. The upper face of the cylinder is maintained at a constant temperature of 400K and the initial temperature of the disc is 300K. If the thermal conductivity of the material of the cylinder is 10W/mK, the specific heat of the material of the disc is 600 J/kg-K, and the time taken for the temperature of the disc to increase to 350K is x min 48sec, then what is the value of x? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to bee thermally insulated except for the upper face of the cylinder.
View Solution
