Infinte number of conducting rods each of length L and thermal con

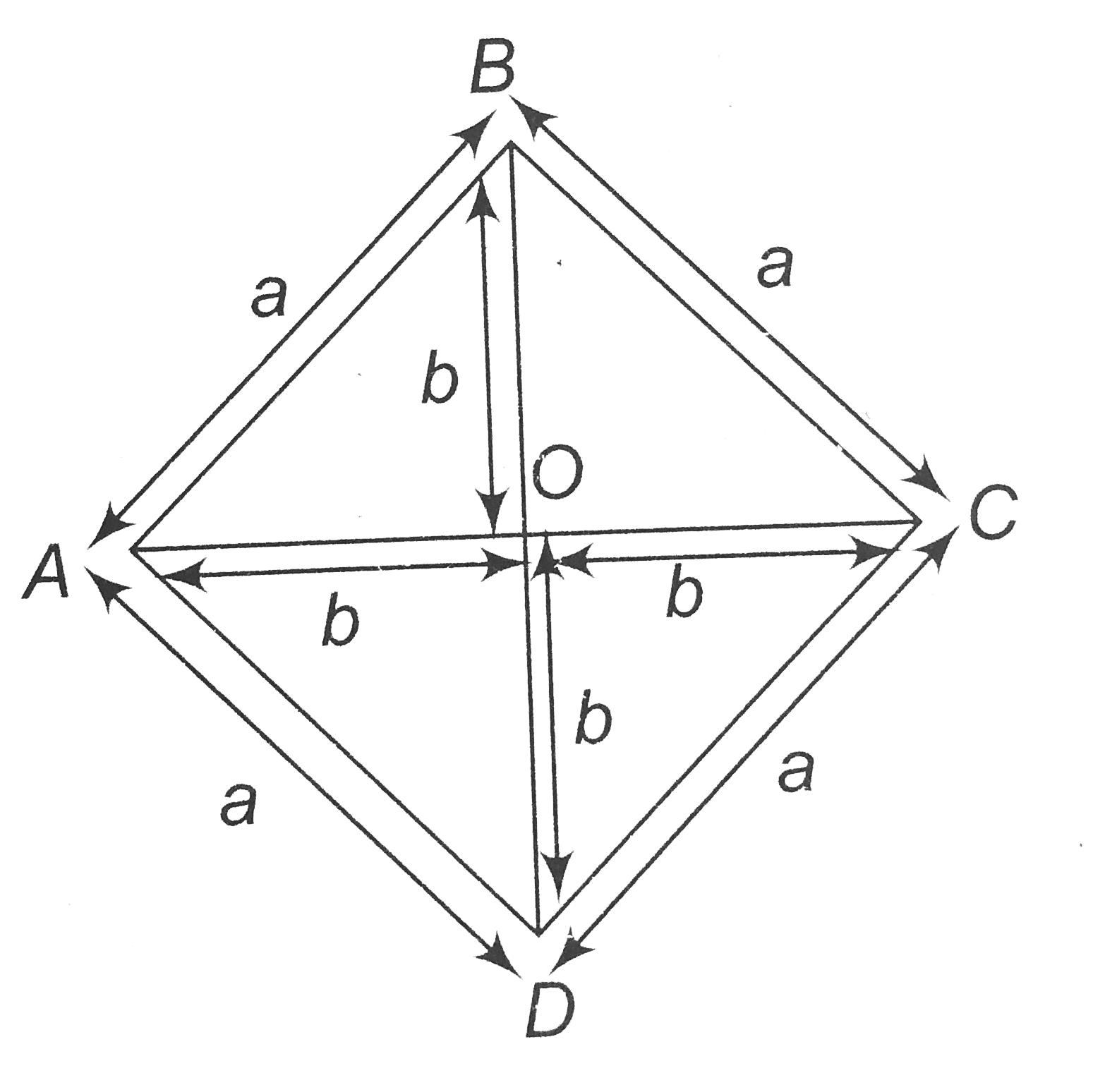
All the rods have same conductance $' K'$ and same area of cross section ' $A'$ . If ends A and C are maintained at temperature $2 T_{0}$ and $T_{0}$ respectively then which of the following is $/$ are correct?

ARate of heat flow through $A B C, A O C and A D C$ is same
BRate of heat flow through $B O and O D$ is not same
CTotal rate of heat flow from $A$ to $C$ is $\frac{3 K A T_{0}}{2 a}$
DTemperature at junctions $B, O and D$ are same
A rod of length l and cross-section area A has a variable thermal conductivity given by K = $α$ T, where $α$ is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature $T_{1}$ and $T_{2}$ $(T_{1} > T_{2})$ . Heat current flowing through the rod will be
A $\frac{A α (T_{1}^{2} - T_{2}^{2})}{l}$
B $\frac{A α (T_{1}^{2} + T_{2}^{2})}{l}$
C $\frac{A α (T_{1}^{2} + T_{2}^{2})}{3 l}$
D $\frac{A α (T_{1}^{2} - T_{2}^{2})}{2 l}$
The two ends of a rod of length $L$ and a uniform cross-sectional area $A$ are kept at two temperature $T_{1}$ and $T_{2}$ $(T_{1} > T_{2})$ . The rate of heat transfer. $\frac{d Q}{d t}$ , through the rod in a steady state is given by
A $\frac{d Q}{d t} = \frac{K L (T_{1} - T_{2})}{A}$
B $\frac{d Q}{d t} = \frac{K L (T_{1} - T_{2})}{L A}$
C $\frac{d Q}{d t} = K L A (T_{1} - T_{2})$
D $\frac{d Q}{d t} = \frac{K A (T_{1} - T_{2})}{L}$

$\frac{2 (T_{2} - T_{1}) A K}{\sqrt{5} L}$