Define monochromatic emissive power of a body. Write the relation between emissive power and radiant emittance.
Text Solution
The radiant energy emitted per second by a unit surface area of the body per unit range of wavelenght is defined as monochromatic emissive power.
Radiant emittance, e=∫λ=0eλdλ where eλ is the emissive power .
|
Topper's Solved these Questions
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - NUMERICAL EXERCISE (LEVEL -1)
8 Videos
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - NUMERICAL EXERCISE (LEVEL -2)
10 Videos
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - TEST YOUR SELF
6 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
- TRANSMISSION OF HEATBOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)
3 Videos
Similar Questions
Knowledge Check
Dimensions of emissive power are
A[M1L0T−3]B[M1L0T−2]C[M0L1T−3]D[M1L1T−1K1]Dimensions of emissive power are
A[M1L−2T−3]B[M1L2T−3]C[M1L0T−3]D[M1L0T−2]Emissive power of a perfectly black body
Ais independent of temperatureBis inversely proportional to fourth power of its temperatureCdecrease with increase in temperatureDdepends on the wavelength of radiation
State the factors which the emissive power of a body depends on.
View SolutionS.I unit of emissive power is
View SolutionThe emissive power of a surface depends upon
View SolutionAt a certain temperature for given wavelength, the ratio of emissive power of a body to emmisve power of black body in same circumstance in known as
View SolutionThe graph shown in the adjacement diagram represents the variation of temperature (T) of two bodies x and y having the same surface area, with time (t). Both of these bodies lose heat only due to the emission of radiation. Find the correct relation between the emissive and absorptive power of the two bodies.
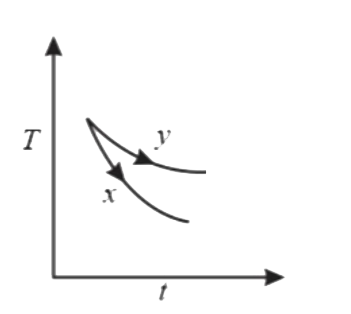
View Solution
