Eleven rods each of length L , cross section A and coeffeicient of thermal conductivity K are arranged as shown . Find the rate of heat transfere from P to Q(T1>T2) .
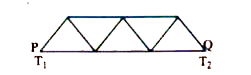
KA(T1−T2)L−12
Topper's Solved these Questions
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
4 Videos
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - NUMERICAL EXERCISE (LEVEL -1)
8 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
- TRANSMISSION OF HEATBOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)
3 Videos
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
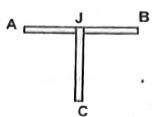
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL
Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material L. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod isA(dQdt)AB=(dQdt)CDB(dQdt)BE=27(T1−T2)KAlC(dQdt)CH≠(dQdt)DGD(dQdt)BC=(dQdt)DC
Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View Solution
Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material k. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod is
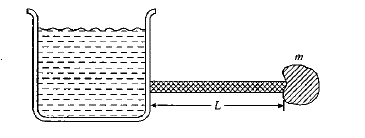
View SolutionFigure-4.13 shows a water tank at a constant temperature. T0 and a small bodyof mass m, and specific heat S at a temperature T1 . Given that T1<T0. A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.

View Solution
