Plot the corresponding reference circle for each of the following simple harmonic motions, indicate the initial (t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti clockwise in every case (x is cm and t is in s)
1) x=−2sin(3t+π/3)
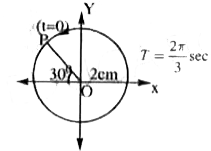
2) x=cos(π/6−t)

3) x=3cos(2πt+π/4)
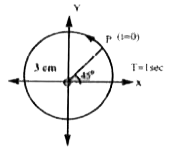
x=2cosπt
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
Plot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial(t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case :(x is in cm and t is in s ).
(a) x=−2sin(3t+π/3) (b)x=cos(π/6−t) (c) x=3sin(2πt+π/4) (d) x=2cosπt
View SolutionPlot the corresponding reference circle for given SHM, indicate the initial (t=0) position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. x=−3sin(2t+π4) (Express in the form , x= Acos ( omega t + phi)).
View Solution
Knowledge Check
A particle in simple harmonic motion is described by the displacement functionx(t)=Acos(ωt+θ). If the initial (t = 0) position of the particle is 1 cm, its initial velocity is it cm/s, and its angular speed is π radian per second then its amplitude is
A1 cmB√2 cmC2 cmD2.5 cmthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
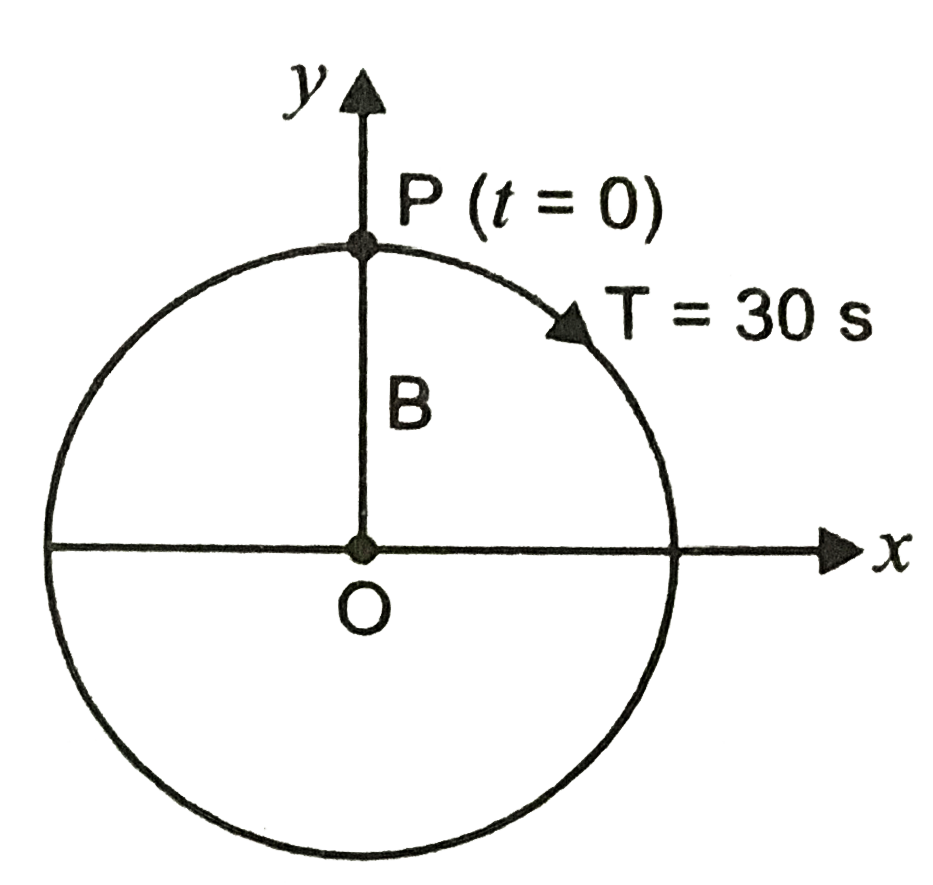 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)Figure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
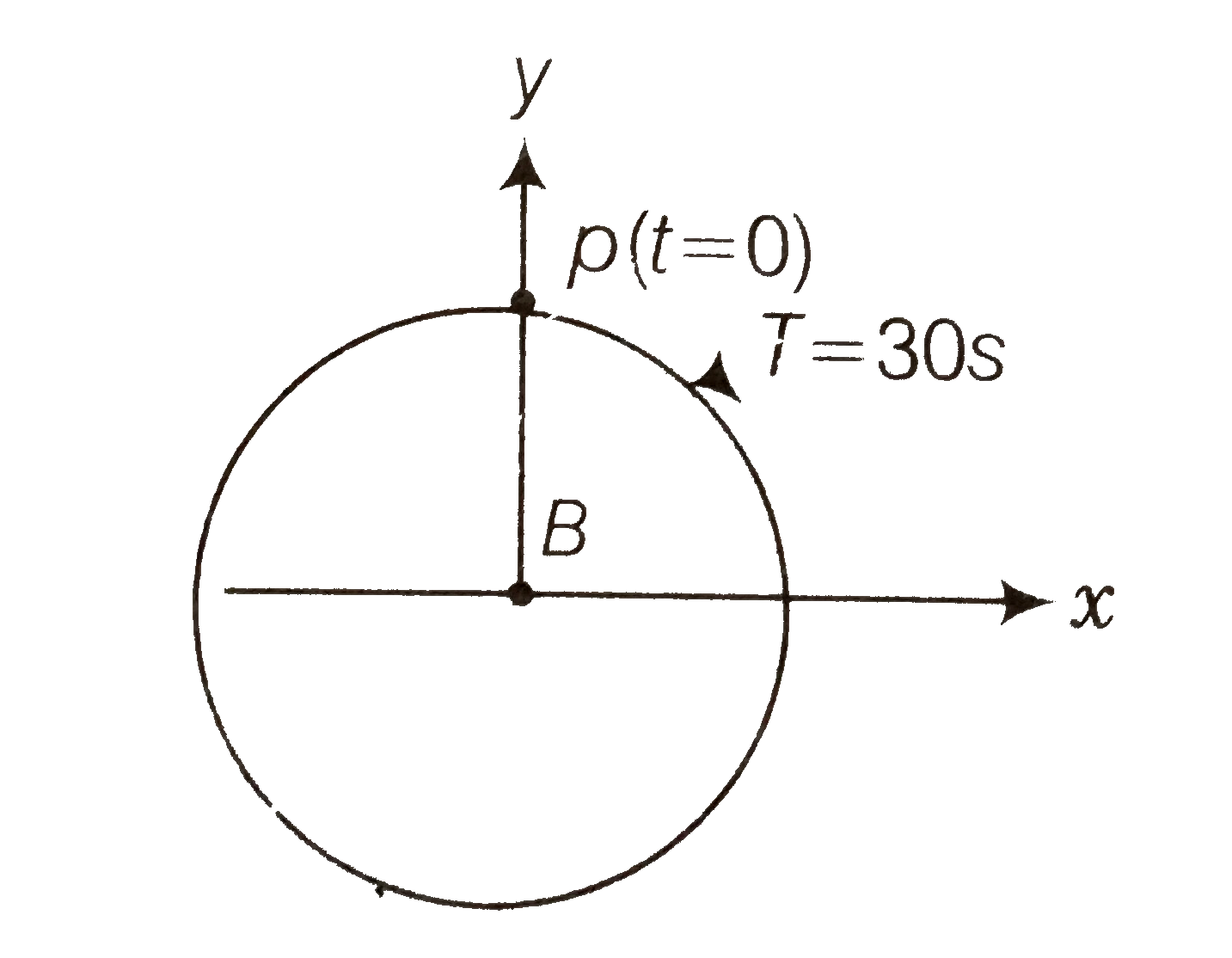 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Plot the corresponding reference circle for given SHM, indicate the initial (t=0) position of the paritcle, the radius of the circle , and the angular speed of the rotating paritcle. Consider anticlockwise direction for rotation. x=−3sin(2t+π4) (Express in the form , x= Acos ( omega t + phi)).
View SolutionPlot the corresponding reference circle for given SHM x=2cos(π3−t) .Indicate the initial (t−0) position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint : x=2cos(π3−t)=2cos(t−π3) as cos(−θ)=cosθ . Compare with x=Acos(ωt+ϕ)
View SolutionPlot the corresponding reference circle for given SHM x=2cos(π3−t) .Indicate the initial (t−0) position of the particle , the radius of the circle and the angular speed of the rotating particle . Consider anticlockwise direction for rotation.
Hint : x=2cos(π3−t)=2cos(t−π3) as cos(−θ)=cosθ . Compare with x=Acos(ωt+ϕ)
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
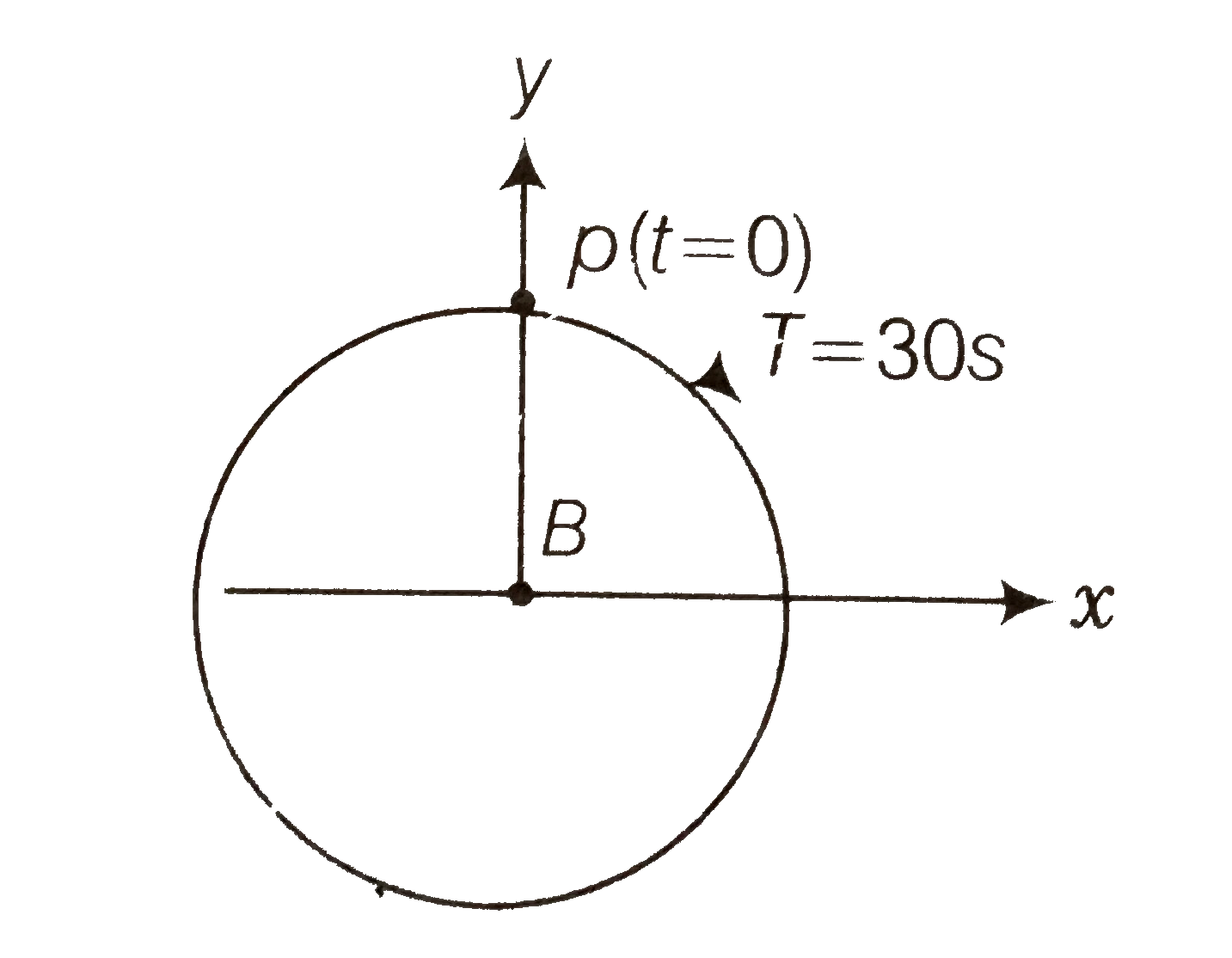
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
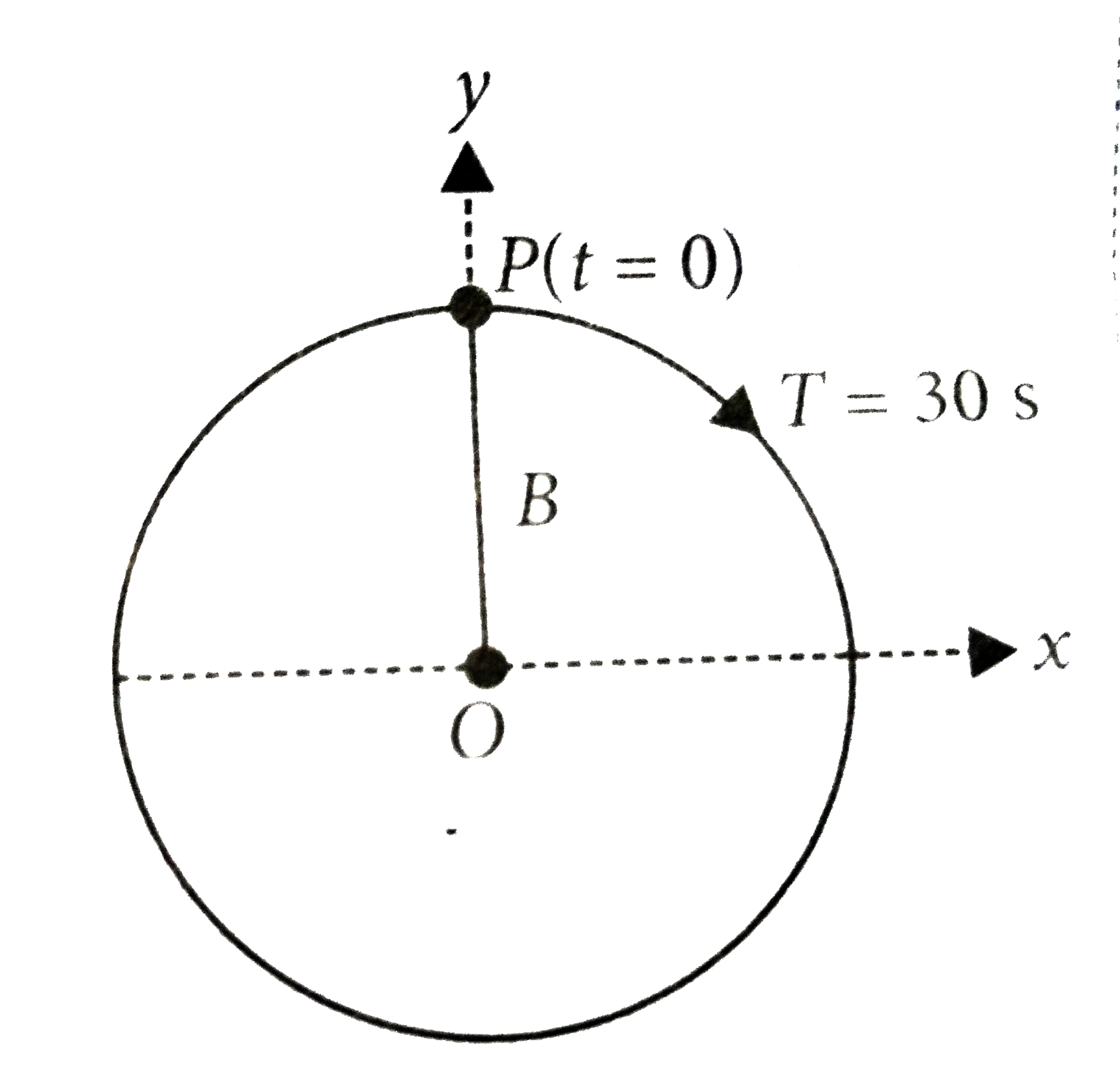
View Solution
