Figure shows the variation of force acting on a particle of mass 400g executing simple harmonic motion. Find the frequency of oscillation of the particle

Text Solution

Verified by Experts

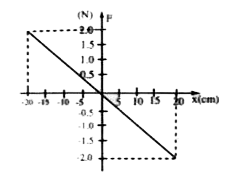
The slope of the graph $= \frac{F}{x} = \frac{0.5}{5} = - 0.1 N c m^{- 1} s = - 10 N m^{- 1}$
But $F = - m ω^{2} x$ or $\frac{F}{x} = - m ω^{2}$
so $- m ω^{2} = - 10$ or $m ω^{2} = 10$ or $ω^{2} = \frac{10}{m}$
$∴ ω^{2} = \frac{10}{4 \times 10^{- 1}} \Rightarrow ω = \frac{10}{2} = 5 ∴ f = \frac{ω}{2 ω} = \frac{5}{2 π} s^{- 1}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
A $4 s^{- 1}$
B $(\frac{5}{2 π}) s^{- 1}$
C $(\frac{1}{8 π}) s^{- 1}$
D $(\frac{1}{2 π}) s^{- 1}$
Question 2 - Select One
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.
BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.
Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.
Dits linear velocity and acceleration always attain their peak values simlataneaously.
Question 3 - Select One
The velocity of a particle executing simple harmonic motion is
A $ω^{2} \sqrt{A^{2} + x^{2}}$
B $ω \sqrt{A^{2} - x^{2}}$
C $ω \sqrt{A^{2} + x^{2}}$
D $ω^{2} \sqrt{A^{2} - x^{2}}$

AAKASH SERIES-OSCILLATIONS-PROBLEM

Home
Ask Doubt
Profile