Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2} = A cos ω t$ are superimposed on a particle of mass m. Find the total mechanical energy of the particle.

Text Solution

Verified by Experts

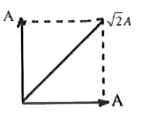
Phase difference between the two SHMs is $90^{\circ}$ Therefore, resultant amplitude is
$A = \sqrt{2 A} E = \frac{1}{2} m ω^{2} A_{R}^{2} = \frac{1}{2} m ω^{2} {(\sqrt{2} A)}^{2} = m ω^{2} A^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184videos
OSCILLATIONS
BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175videos
OSCILLATIONS
BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49videos
OSCILLATIONS
BOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12videos
OSCILLATION
BOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5videos
PHYSICAL WORLD

Similar Questions

Knowledge Check

Question 1 - Select One
Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2}$ = Acos $ω$ t are superimposed on a particle of mass m. The total mechanical energy of the particle is
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero
Question 2 - Select One
Two simple harmonic motion $y_{2} A sin ω t$ and $y_{2} = A cos ω t$ are superimposed on a particle of mass $m$ . The total mechanical energy of the particle is:
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero
Question 3 - Select One
Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2} = A cos ω t$ are supre imposed on a particle of mass m.
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero

AAKASH SERIES-OSCILLATIONS-PROBLEM

Home
Ask Doubt
Profile