An iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20∘C. The temperature at which (both for ball and plate) the ball just pass through the hole is (αiron=12×10−6/1∘C,αbrass=18×10−6/1∘C)Solution in Telugu
68∘C
48∘C
28∘C
40∘C
The correct Answer is:B
Step by step video, text & image solution for An iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20^(@) C. The temperature at which (both for ball and plate) the ball just pass through the hole is (alpha_("iron") = 12 xx 10^(-6) //1^(@) C, alpha_("brass") = 18 xx 10^(-6) //1^(@) C) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-I (Straight Objective Type Questions) Mechanics & Elasticity application4videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Geometry Applications5videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (LECTURE SHEET) Integer Type Questions5videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
If a cylinder of diameter 1.0cm at 30°c is to be slide into a hole of diameter 0.9997 cm in a steel plate at the same temperature, then minimum required rise in the temperature of the plate is [coefficient of linear expansion of steel =12×10−6/∘C ]
05:48View SolutionThe temperature compensated pendulum is designed to compensate for the change in length due to temperature rise. Figure shows one such pendulum. It consists of an isosceles triangular frame as shown in the figure. The pendulum is supported at mid-point of side AB, and it remains horizontal. Determine the ratio (l1/l2)2, so that the length of the pendulum remains same at all temperatures.
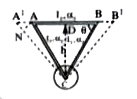 04:37View Solution
04:37View SolutionA block is hanged by means of two identical wires having cross-section area A (1mm2) as shown in the figure. If temperature is lowered by ΔT(10∘C), find the mass (in kg) to be added to hanging mass such that junction remains at its initial positions. Given that coefficient of linear expansion α=2×10−5I0C and Young's modulus Y=5×1011N/m2 for the wire.
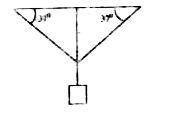 03:53View Solution
03:53View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
03:46View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
View SolutionAn iron ball has a diameter of 6cm and is 0.010mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 30∘C. At what temperature, the same for ball and plate, will the ball just pass through the hole?
Take the values of (prop) from Table 20.2.View SolutionAn iron ball (coefficient of linear expansion =1.2xx(10^(-5)//^(@)C ) has a diameter of 6 cm and is 0.010 mm too large to pass through a hole in a brass plate (coefficient of linear expansion =1.9xx10^-5//^(@)C ) when the ball and the plate are both at a temperature of 30^@C At what common temperature of the ball and the plate will the ball just pass through the hole in the plate ?
09:09View SolutionAn iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20^(0)C . The temperature at which (both for ball and plate) the ball just passes through the hole is (alpha_(iron) = 12 xx 10^(-6 //0)C, alpha_(brass) = 18 xx 10^(-6 //0)C)
09:09View SolutionA cylindrical steel plug is inserted into a circular hole of diameter 2.60 cm in a brass plate. When the plug and the plates are at a temperature of 20^(@)C, the diameter of the plug is 0.010 cm cmaller than that of the hole. The temperature at which the plug will just fit in it is ("Given",alpha_(steel)=(11xx10^(-6))/("^(@)C)and alpha_(bress)=(19xx10^(-6))/C)
02:16View SolutionThe length of a brass rod at 20^@C is observed to be 0.8 m when measured by an iron scale, correct at 0^@C . What will be the correct length of the rod at 0^@C ? Take, alpha_("iron") = 1.2 xx 10^(-5) ""^@C^(-1) alpha_("brass") = 1.9 xx 10^(-5) ""^@C^(-1)
05:02View SolutionAn iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20∘C. The temperature at which (both for ball and plate) the ball just pass through the hole is
(αiron=12×10−6/1∘C,αbrass=18×10−6/1∘C)05:07View SolutionAn iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20∘C. The temperature at which (both for ball and plate) the ball just pass through the hole is (αiron=12×10−6/1∘C,αbrass=18×10−6/1∘C)
03:38View SolutionAn iron ball of diameter 6cm and is 0.01 mm too large to pass through a hole in a brass plate when the ball and plate are at a temperature of 20∘C. The temperature at which (both for ball and plate) the ball just pass through the hole is (αiron=12×10−6/1∘C,αbrass=18×10−6/1∘C)
02:46View SolutionWhen a brass rod is put in a furnace, its length increases by 1 %. If the room temperature is 25°C and αBrass=20×10−6/∘C, the change in. the temperature is 100x∘C, where x=
02:45View SolutionThe difference between the lengths of steel rod and a brass rod is 0.6 at all temperatures. What are their lengths at 0^@C ? (alpha_Steel = 12 xx 10^-6//^@C , (alpha_(brass)= 18 xx 10^-6//^@C )
08:52View Solution

