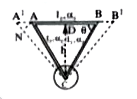
The temperature compensated pendulum is designed to compensate for the change in length due to temperature rise. Figure shows one such pendulum. It consists of an isosceles triangular frame as shown in the figure. The pendulum is supported at mid-point of side AB, and it remains horizontal. Determine the ratio (l1/l2)2, so that the length of the pendulum remains same at all temperatures.
α1α2
α12α2
2α2α1
4α2α1
The correct Answer is:D
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Mechanics applications
4 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (More than One correct answer Type Questions)
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-I (Straight Objective Type Questions) Mechanics & Elasticity application
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 3
33 Videos
Similar Questions
The compensated pendulum of a clock consista of an isosceles triangular frame of base length l1 and expansivity α1 and side length l2 and expansivity α2. The pendulum is supported as shown in the figure. Calculate the ratio l1/l2 so that the length of the pendulum may remain unchanged at all temperatures?

View SolutionA simple pendulum consists of an inextensible string of length L and mass M. The oscillating pendulum is suspended inside a stationary lift. The lift then started descending with an acceleration 3.4m/s2. Will its time period increase, decrease or remain same?
View Solution
Knowledge Check
A 1N pendulum bob is held at an angle θ from the vertical by a 2 N horizontal force F as shown in the figure. The tension in the string supporting the pendulum bob (in newton) is
 AcosθB2cosθC√5D1
AcosθB2cosθC√5D1The l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
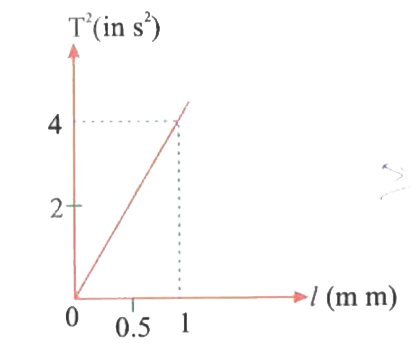 A1sB1.2 sC√2 sD1√2s
A1sB1.2 sC√2 sD1√2sIf the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
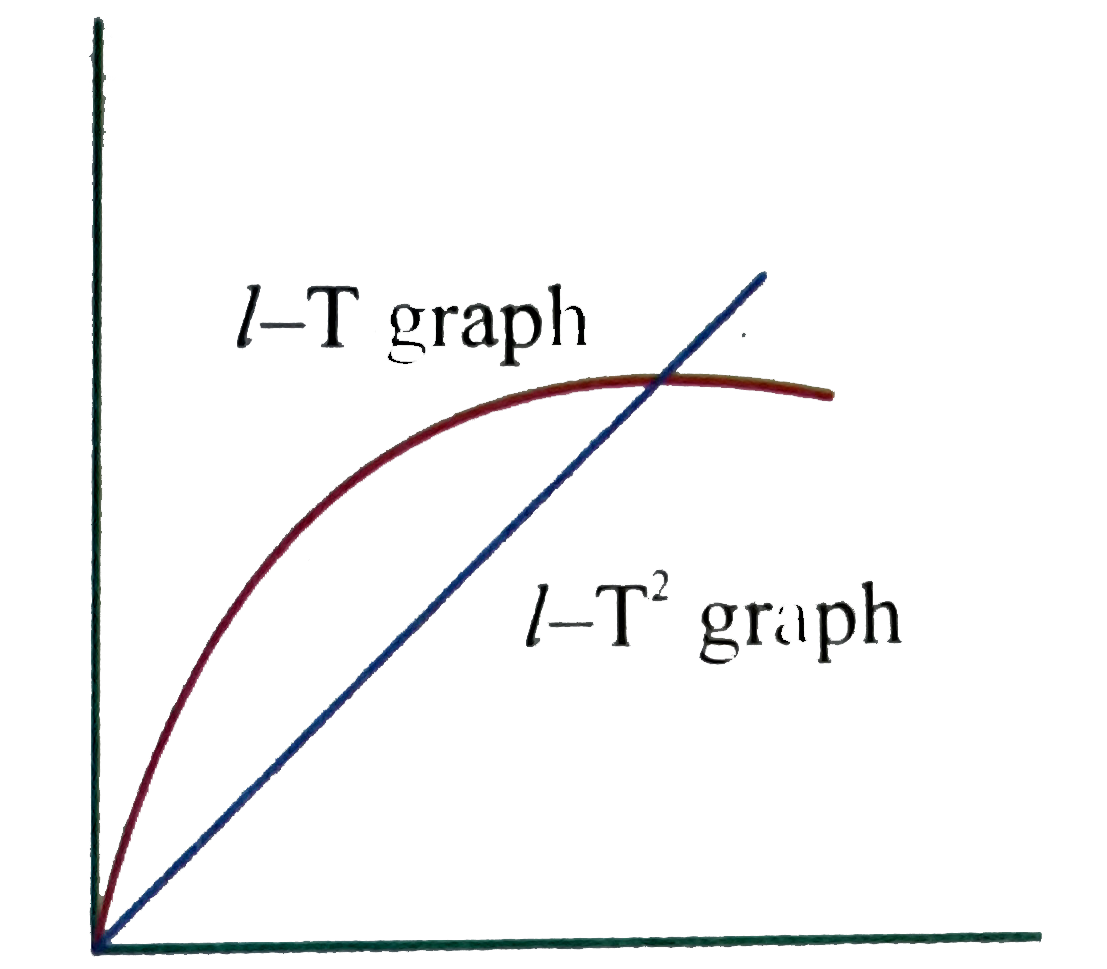 A25cmB21cmC22cmD27cm
A25cmB21cmC22cmD27cm
l - T and l−T2 graphs of a simple pendulum on earth are as shown in the figure. The x-coordiante (OA) of point of intersection of the graphs is nearly equal to (on the earth g=9.8ms−2)
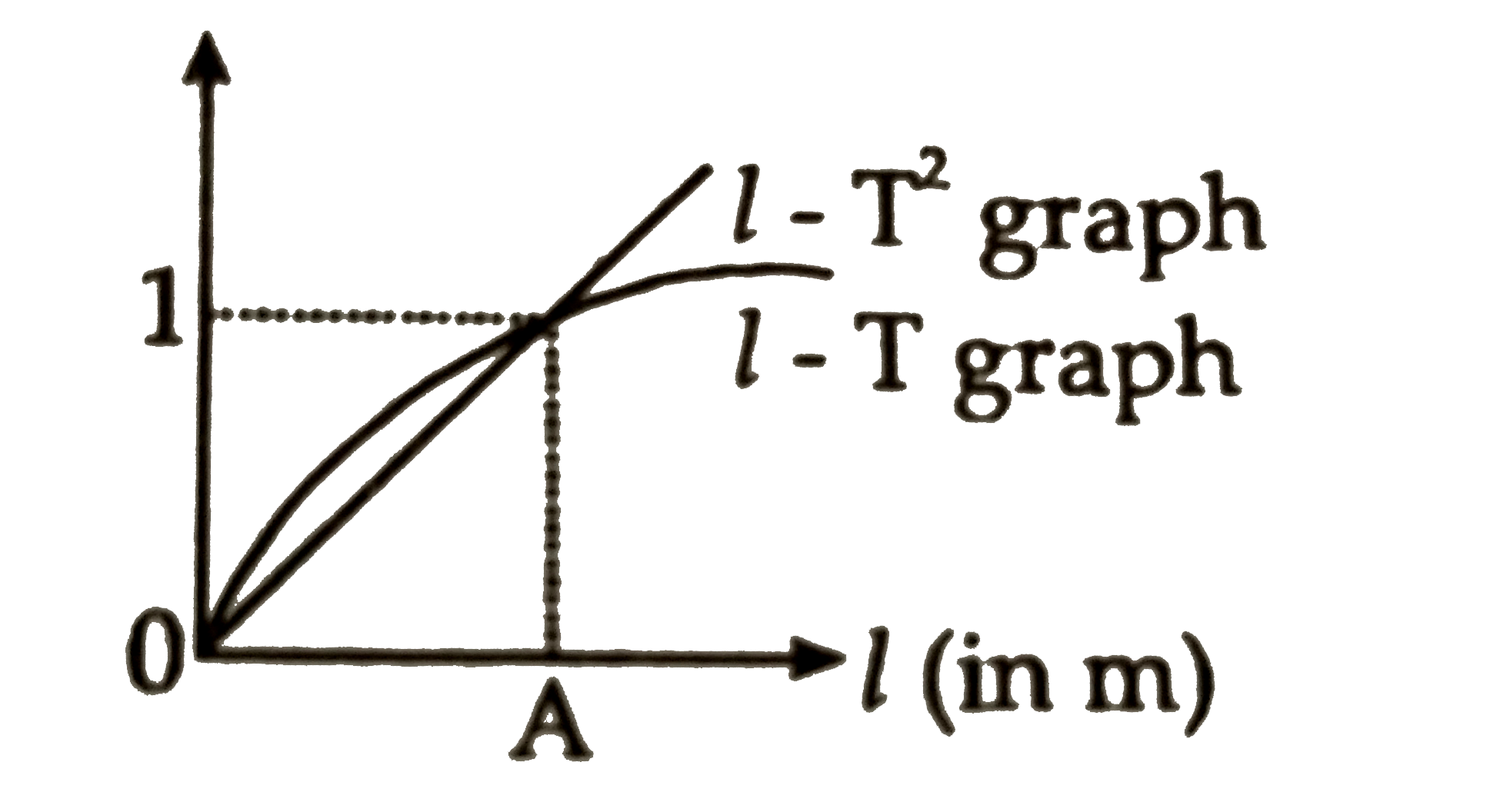
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionFig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
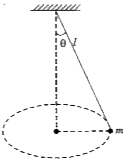
View SolutionA 1N pendulum bob is held at an angle θ from the vertical by a 2N horizontal force F as shown in figure. The The tension in the string supporting the pendulum bob (in newton) is
 .
.
View Solution
