The system shown consists of two springs. If the temperature of the rod is increased by ΔT. the compression in the left spring is (assume the thermal stress in the rod is zero)

Lα(ΔT)4
3Lα(ΔT)4
Lα(ΔT)3
zero
The correct Answer is:B
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (More than One correct answer Type Questions)
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Linked Comprehension Type Questions)
7 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Straight Objective Type Questions) Geometry Applications
5 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 3
33 Videos
Similar Questions
The system shown is figure consists of 3 springs and two rods. If the temperature of the rod is increased by ΔT, then the total energy stored in three springs is β×99484kL2α2(ΔT)2. Determine the value of β. The spring are initially relaxed and there is no friction anywhere. For rod the coefficient of linear expansion is α
_E01_089_Q01.png)
View SolutionThe systeam shown is figure consists of 3 springs and two rods. If the temperature of the rod is increased by ΔT, then the total energy stored in three springs is β×99484kL2α2(ΔT)2. Datermine the value of β. The soring are initially relaxed and there is no frication anywhere. For rod the coefficient of linear expansion is α
_E01_089_Q01.png)
View Solution
Knowledge Check
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTαThe moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTαA rod of aluminium is fixed between two rigid support. If the temperature of rod is increased by 10°C, then the thermal stress on the rod is (Take Y=7×1010Pa and α=2.4*10−5K−1)
A1.4×103 PaB1.7×107 PaC1.7×103 PaD2.4×107 Pa
The system shown in figure consists of three springs and two rods as shown. If the temperature of the rods is increased by δ(t) calculate the energy stored in each of the springs. The springs are initially relaxed. There is no friction.
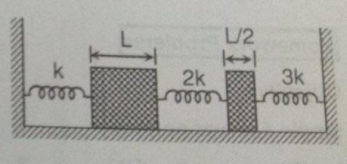
View SolutionThe moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View SolutionThe moment of inertia of a rod about its perpendicular bisector is l, when temperature of rod is increased by ΔT, the increase in the moment of inertia of the rod about same axis (γ = temperature coefficient of volume expansion)
View SolutionA rod of aluminium is fixed between two rigid support. If the temperature of rod is increased by 10°C, then the thermal stress on the rod is (Take Y=7×1010Pa and α=2.4*10−5K−1)
View SolutionTwo rods of material X sandwich another rod of material Y as shown in figure. At temperature t, the three rods are in a state of zero strailn and of length L and riveted to each other in this state. If the temperature of the system increases to T+ΔT, find the final length of the system of the three rods. Given that the coefficients of linear expansions of the roods and their Young's modulus for material X and Y are alpnax,αy,Yx and Yy respectively. Consider αy>αx.

View Solution
