A vertical cylinder of height 100cm contains air at a constant temperature and its top is closed by a frictionless pistion at atmospheric pressure (76cm of Hg) as shown figure (a). If mercury is slowly poured on the pistion, due to its weight air is compressed. Find the maximum height of the mercury column which can be put on the pistion.
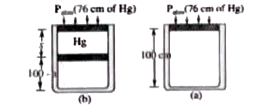
12 cm
24 cm
36 cm
48 cm
The correct Answer is:B
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Kinetic theory of gases)
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF GASES (LECTURE SHEET) More than One correct answer Type Questions
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH SERIESChapter:THERMAL PROPERTIES OF MATTERExercise:EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Ideal Gas equation - applications)
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH SERIESChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE EXERCISE
Explore 99 Videos
- THERMODYNAMICSBook:AAKASH SERIESChapter:THERMODYNAMICSExercise:EXERCISE - 3
Explore 33 Videos
Similar Questions
A vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) asshown in figure-2.12. If mercury is slowly poured on the piston, due to its weight airis compressed. Find the maximum height of the mercury column which can be put on the piston.
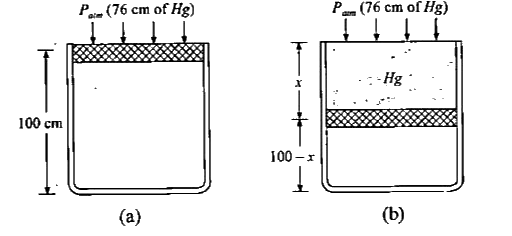
View SolutionA vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
View Solution
Knowledge Check
Atmospheric pressure is 76 cm Hg and pressure of the gas is 77 cm Hg. Hence, height, 'h' of the mercury column in open arm is
A1 cmB113.6×980cmC153 cmD1×1.36×980 cmThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
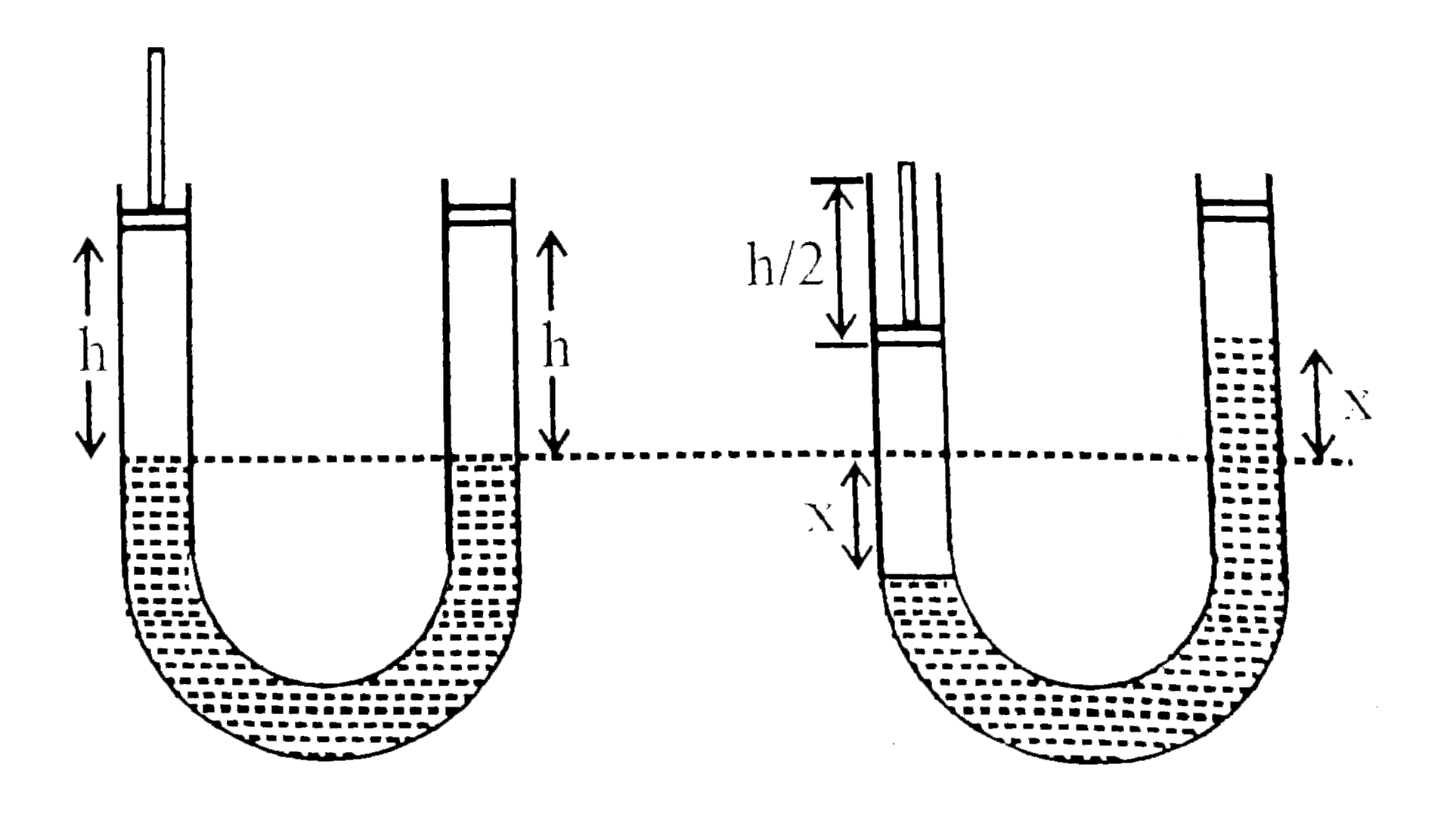
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure thenAhP0=(h2+x)P1BhP0=(h−x)P2CP1=P2DP1−P2=2xpg where p is density of mercuryA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
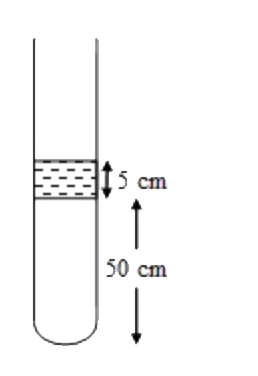 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cm
A vertical cylinder of total length 100 cm is closed at the lower end and is fitted with a movable frictionless gas tight disc at the other end. An ideal gas is trapped under the disc. Initially the height of the gas column is 90 cm when the disc is in equilibrium between the gas and the atmosphere. Mercury is than slowly poured on the top of the disc and it just starts overflowing when the disc has descended through 32 cm. Find the atmospheric pressure (in cm of Hg). Assume that the temperature of the gas to remain constant and neglect the thickness and weight of the disc. Give your answer excluding the decimal places.

View SolutionA vertical cylinder of total lwgth 100 cm is closed at the lower end and fitted with a movable , frictionless, gas - tight disc ,at the other end. An ideal gas is trapped under the disc of negligible mass. Initially the height of the gas column is 90 cm and the dis is in equlibrium . Mercury is slowly poured on the top of the disc and it just starts overflowing when the disc has descended thorugh 32 cm. find the atmospheric pressure.
View SolutionThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
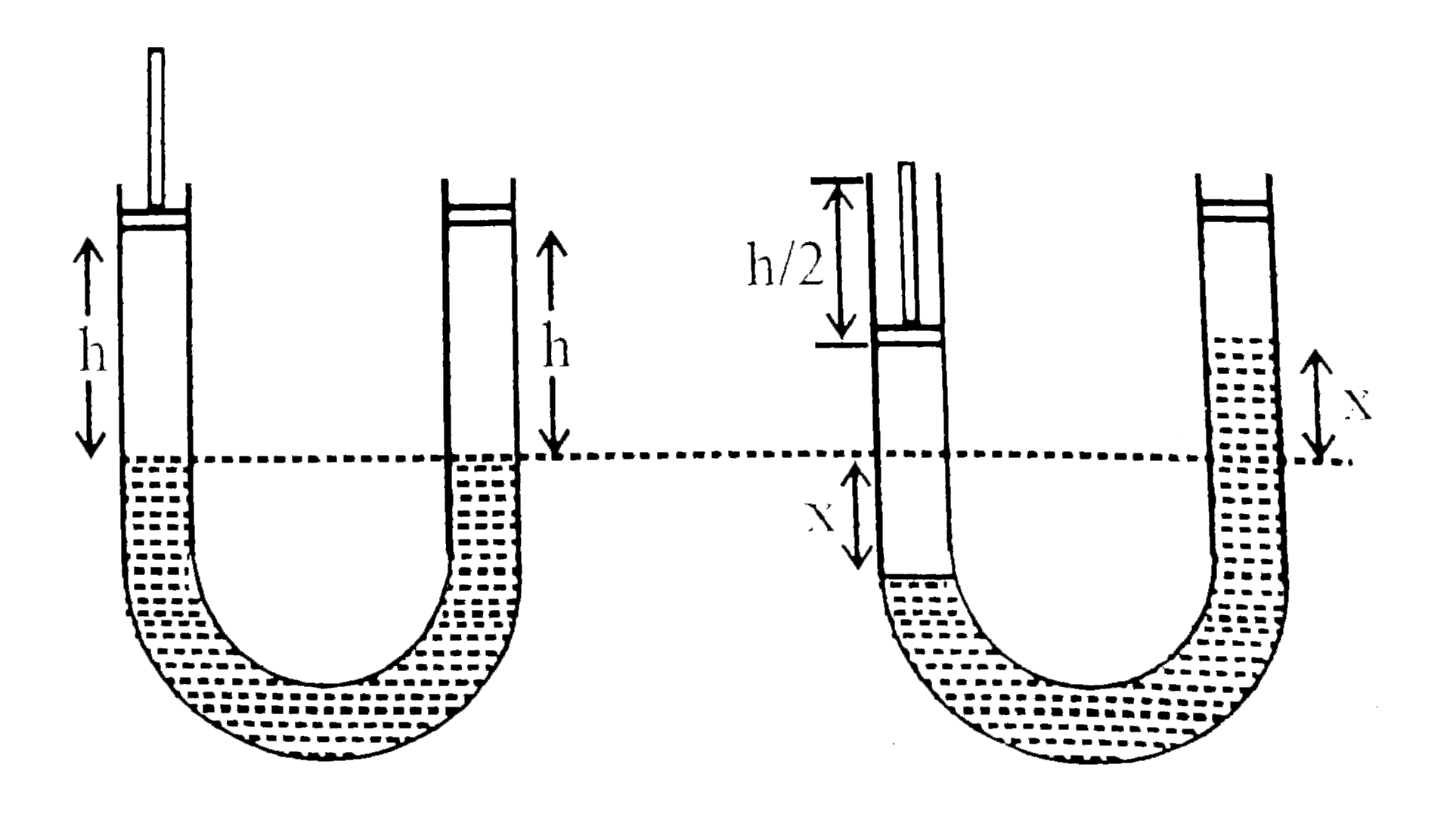
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure then
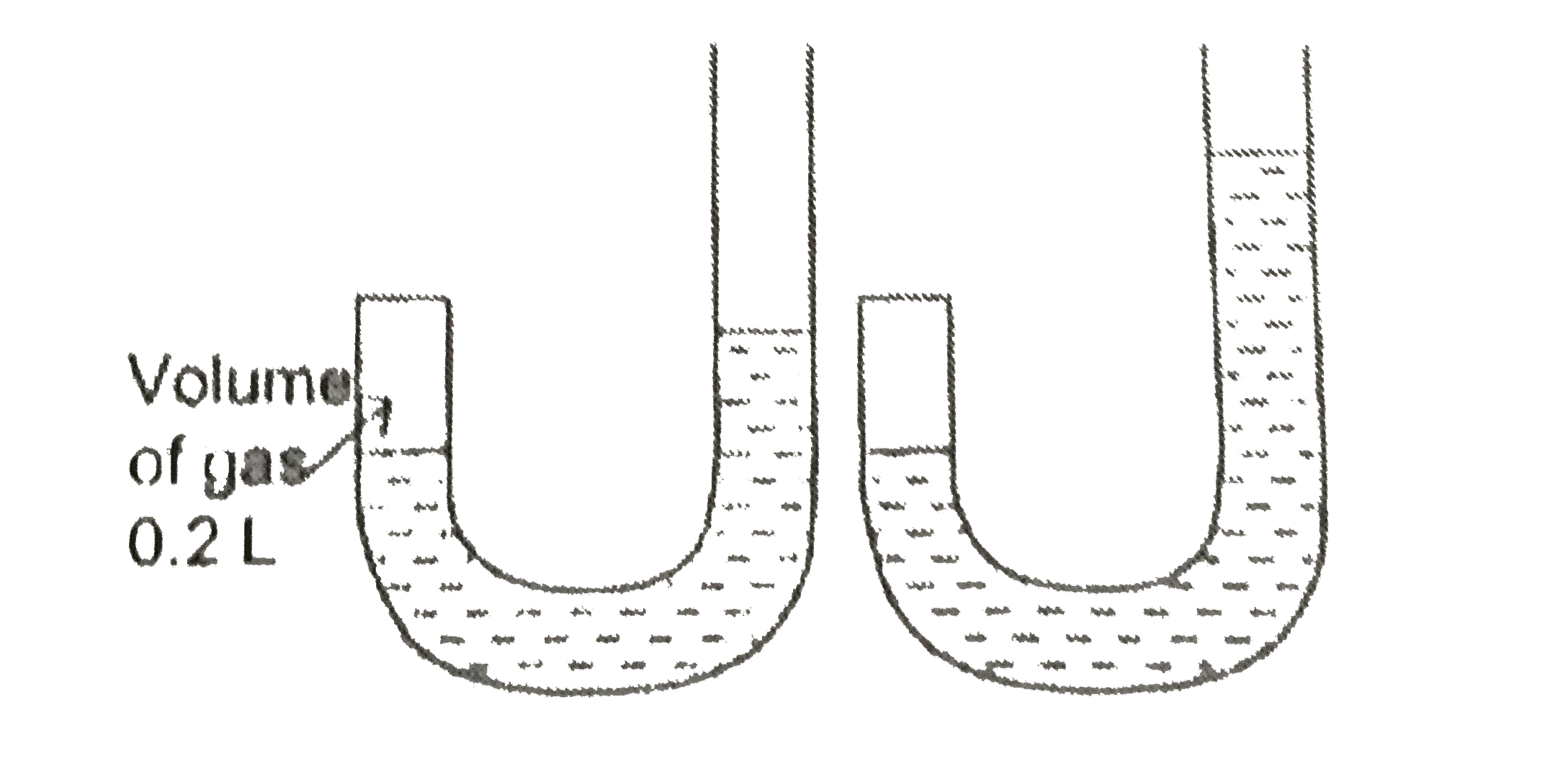
View SolutionJ-shped tube closed at one end was used by Boyle to study the relationship between the pressure of the trapped gas and its volume. Such a set up is given here. Initially some amount of gas is taken in the tube and mercury is poured in it. The volume of the gas is 0.2 L and the difference in the height of the mercury column is 760 mm of Hg. Now, some more amount of mercury is poured and the difference in the height of the mercury column is found to be 1140 mm of Hg. Calculate the new volume of the gas considering the temperature constant.
View SolutionA horizontal tube of 1m is closed at both ends. A mercury column of 20 cm is contained in the middle of the tube and two equal lengths of this tube contain air at an atmospheric pressure of 76cm. The tube is now placed vertically. Calculate the distance through which the mercury column will be displaced at a constant temperature.
View Solution
