A horizontal tube of 1m is closed at both ends. A mercury column of 20 cm is contained in the middle of the tube and two equal lengths of this tube contain air at an atmospheric pressure of 76cm. The tube is now placed vertically. Calculate the distance through which the mercury column will be displaced at a constant temperature.

Let M and N are two parts of tube at the left and right sides of O.
Case (i) : When tube is horizontal,
Lengths of M and N =40cm
Pressure of M and =76 cm of Hg
Case (ii): Let the tube is inverted and placed in vertical position.
Let the mercury column is displaced by a distance y by placing tube vertically
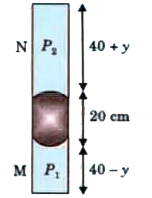
Lengths of M and N are (40-y) and (40+y) respecively.
P1= Preessure of par M
P2= Pressure of part N
As temperature is constant
Therefore, we can write PV=constant
For M: P0(40A)=P1(40−y)A
⇒P1=P0(40)(40−y).......(i)
For N: P0(40A)=P2(40+y)A
⇒P2=P040(40+y)...........(ii)
Here A= area of cross section of tube
Pressure at lower face (P1)=Pressure at upper face (P2)+ Pressure due to mercury column of height 20 cm.
P1=P2=20pg........(iii)
Use (i) and (ii) in (iii)
P040(40−y)=P040(40+y)+20pg
40P0(40−y)−40P0(40+y)=20pg
40×76pg[2y1600−y2]=20pg
(52)(2y)=1600−y2
304y=1600−y2
y2+304y−1600=0
Solving for y, we get y=5.18 cm
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Textbook Exercises)
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Additional Exercises)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A thin tube sealed at both ends is 90 cm long. It is kept horizontally, the middle 10cm containing mercury and the two equal ends containing air at standard atmospheric pressure. The tube is turned and kept in vertical position. By what amount will the mercury be displaced?
View SolutionA thin tube, sealed at both ends, is 100cm long. If lies horizontally, the middle 10cm containing mercury and the two equal containing air at stan-dard atmospheric pressure. If the tube is now turned to a verical position, by what amount will the mercury be displaced ?
View Solution
Knowledge Check
A vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
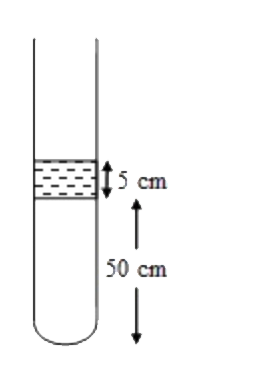 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cmA thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
A75.4B45.8C67.5D89.3
A vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)

View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionA 10 cm long column of Hg is kept in the middel of a narrow 1 m long tube (both eads closed). The two halves of the tube contains air at a pressure of 76 cm of Hg. Calculate the distance (in cm) when the column of Hg be displaced if the tube is held vertical? Answer should be the closest integer.
View SolutionOne metre long tube, closed at both ends, is lying horizontally. A mercurry column of length 0.1 m is filled in its middle and in rest two parts air is filled at atmospheric pressure. What will be the displancement of the mercurry column when the tube is turned to vertical position ? Atmospheric pressure = 0.76 m of Hg.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View Solution
