What do you understand by "sharpness of resonance" in a series LCR circuit ? Find expression for Q-factor of the circuit.
We know that current amplitude in a series LCR circuit is maximum when ω=ω0=1√LC. The maximum value of current at resonance is (Im)rms=VmR For any other value of ω , the current amplitude is less. Choose values of o for which current amplitude is 1√2(Im)max . In Fig. 7.34, these values of ware represented by points B and C having angular frequencies ω1 and ω2 such that ω1=ω2 and ω2=ω0+Δω. The quantity ω02.Δω is regarded as a measure of sharpness of resonance and is also known as the Q-factor of the circuit. Smaller the value of Aw, sharper is the resonance.
It can be easily calcualted that Δω=R2L

∴ Q-factor representing the sharpness of resonance
Q=ω02Δω=ω0LR
As, ω0=1√LC, hence, Q=1√LC.1R=1R√LC
Topper's Solved these Questions
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:LONG ANSWER QUESTIONS -II
Explore 12 Videos
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:SELF ASSESSMENT TEST (SECTION -A) (MULTIPLE CHOICE QUESTIONS)
Explore 4 Videos
- ALTERNATING CURRENT Book:U-LIKE SERIESChapter:ALTERNATING CURRENT Exercise:SHORT ANSWER QUESTIONS
Explore 32 Videos
- ATOMSBook:U-LIKE SERIESChapter:ATOMSExercise:SELF ASSESSMENT TEST (SECTION C)
Explore 2 Videos
Similar Questions
Knowledge Check
In a series LCR circuit, at resonance the
Atotal inpedance is Lω−(1/Cω)Btoal impedance is RCvoltage across C and L are in phaseDthe voltage across C lags the source voltage by π/2Resonance occur in a series LCR . Circuit when :
AXL=XCBXL>XCCXL<XCDnone of theseIn series LCR circuit at resonance,
Acurrent is maximum and impedance is maximumBcurrent is maximum and impedance is minimumCcurrent is minimum and impedance is maximumDcurrent is minimum and pmpedance is minimum
Answer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
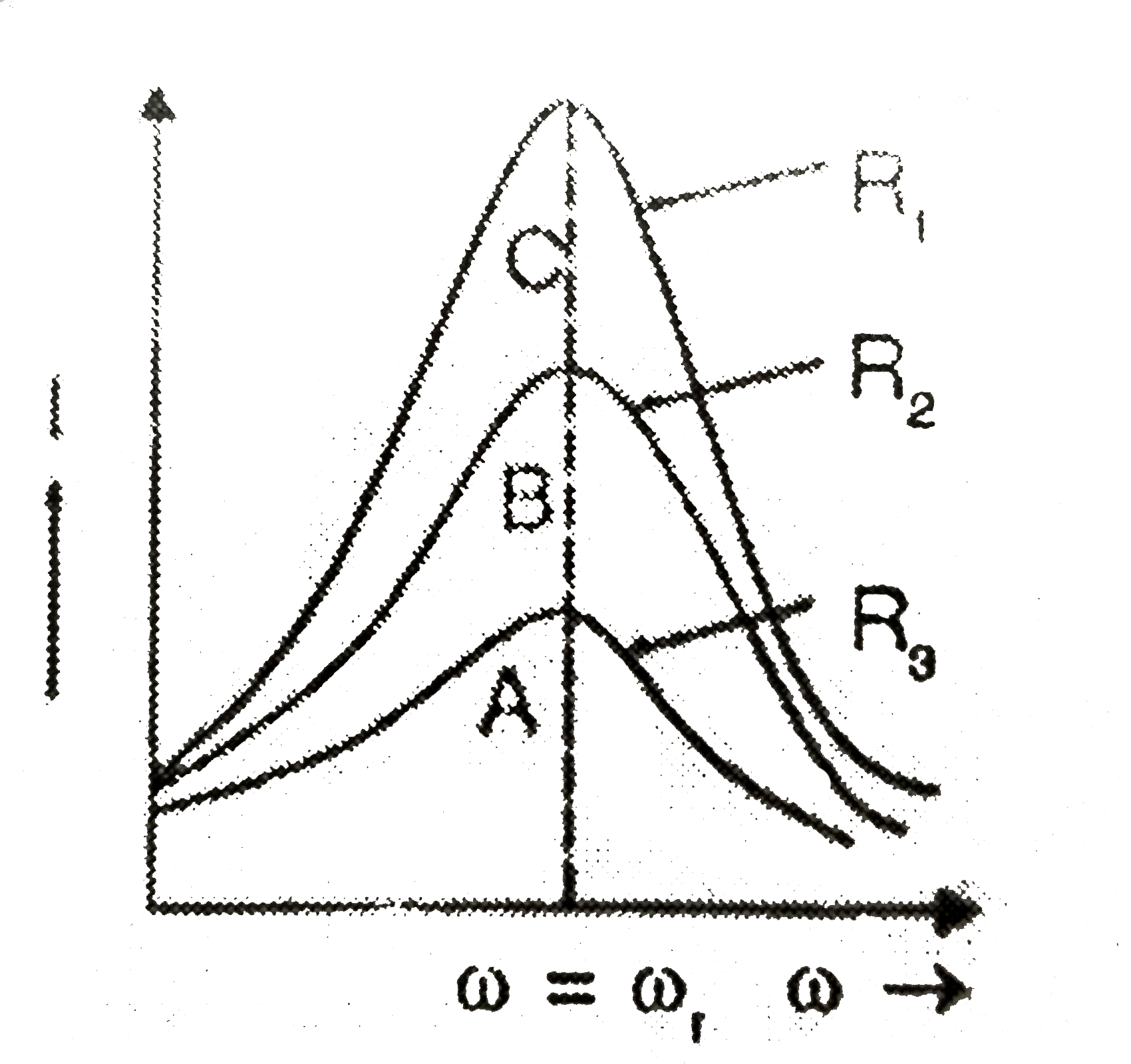
View SolutionResonance in series LCR circuit and quality factor
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionIn a series LCR circuit, obtain an expression for the resonant frequency.
View Solution
