A string 120 cmin length sustains a standing wave, with the points ofstring at which the displacement amplitude is equal to √2mm being separated by 15.0 cm, Find the maximum displacement amplitude. Also find the harmonic corresponding to this wave.
From figure. Point A, B, C, D and E are having equal displacement amplitude.
Further, xE−xA=λ=4×15=60cm
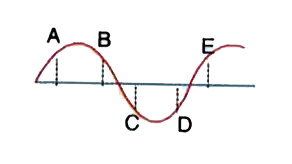
As λ=21n=2×120n=60
∴n=2×12060=4
So, it corresponds to 4th harmonic.
Also, distance of node from A is 7.5 cm and no node is between the.Taking node at origin, the amplitude of stationary wave can be written as, a = A sin kx
Here a=√2mm,k=2πλ=2π60andx=7.5cm
∴√2=Asin(2π60×7.5)=Asinπ4
Hence, A = 2 mm
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)1videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)25videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)10videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)20videos
WAVE OPTICS
Similar Questions
A string 120cm in length sustains a standing wave with the points of the string aat which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View SolutionA string 120cm in length sustains a standing wave, with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude. To which overtone do these oscillations correspond ?
View Solution
Knowledge Check
- Question 1 - Select One
A standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if 5√3mm. The distance between two nearest points, within the same loop having the same displacement amplitude of 5√3 is 10 nm.
The maximum displacement amplitude of the particle in the string is,:A10 mmB(20/√3) mmC10√3D20 mm
A string 120cm in length sustains a standing wave, with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude. To which overtone do these oscillations correspond ?
View SolutionA string 120cm in length sustains a standing wave with the points of the string aat which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View SolutionA string 120 cm in length sustains standing wave with the points of the string at which the displacement amplitude is equal to 3.5 mm being separated by 15.0 cm. The maximum displacement amplitude is X. 95 mm then find out the value of X.
View SolutionA string 120cm in length sustains a standing wave with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 1.50cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View SolutionA stretched string of length 200cm supports a stationary wave with points having a displacement amplitude of mm being separated by equal intervals of 20cm. To which overtone do these vibrations belong.
 View Solution
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x)whereyismeasured∈10^-5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View Solution
