A string 120 cm in length sustains standing wave with the points of the string at which the displacement amplitude is equal to 3.5 mm being separated by 15.0 cm. The maximum displacement amplitude is X. 95 mm then find out the value of X.
In this problem two cases are possible
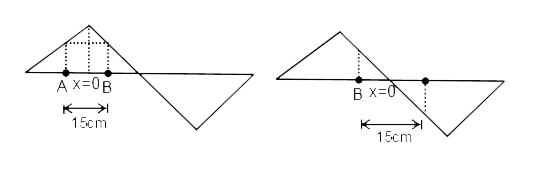
Case-I is that A and B have the same displacement amplitude and Case-2 is that C and D have the same amplitude viz 3.5 mm. In case 1, if x = 0 is taken at antinode then
A = a cos kx In case -2, if x = 0 is taken at node, then A = a sin kx But since nothing is given in the question. Hence from both the cases, result should be same. This is possible only when a cos kx = a sin kx
or kx=π4ora=Acoskx=3.5cosπ/4=4.95mm
Topper's Solved these Questions
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -1 (Objective Problems JEE Main)
35 Videos
- WAVESBOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -2 (Level -I) (Objective Problems JEE Main)
30 Videos
- WAVE OPTICS BOOK - MOTIONCHAPTER - WAVE OPTICS EXERCISE - EXERCISE - 4 (Level - II) Previous Year | JEE Main
16 Videos
- WORK, POWER & ENERGY BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 3 Section-B
22 Videos
Similar Questions
A string 120cm in length sustains a standing wave, with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude. To which overtone do these oscillations correspond ?
View SolutionA string 120cm in length sustains a standing wave with the points of the string at which the displacement amplitude is equal to 3.5mm being separated by 1.50cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View Solution
Knowledge Check
A standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if 5√3mm. The distance between two nearest points, within the same loop having the same displacement amplitude of 5√3 is 10 nm.
The maximum displacement amplitude of the particle in the string is,:A10 mmB(20/√3) mmC10√3D20 mm
Two sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves.

View SolutionA wave travelling on a string at a speed of 10ms−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
View SolutionA point performs damped oscilaltions with frequency ω and dampled coefficient β. Find the velocity amplitude of the point as a function of time t if at the moment t=0
(a) its displacement amplitude is equal to a0,
(b) the displacement of the point x(0)=0 and its velocity projection vx(0)=.x0
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x = 0 and the other is at x=l. When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View SolutionA string of length l and mass m is fixed at both ends with tension t and excited in its fundamental mode.The maximum displacement at the mid point is A Find (a) the maximum kinetic energy of the string ,9b0 the mean kinetic energy of the srting averaged over one oscillation period
hint Take sine distribution of amplitudes
View Solution(i) The equation of wave in a string fixed at both end is y=2sinπtcosπx. Find the phase difference between oscillations of two points located at x=0.4m and x=0.6m.
(ii) A string having length L is under tension with both the ends free to move. Standing wave is set in the string and the shape of the string at time t=0 is as shown in the figure. Both ends are at extreme. The string is back in the same shape after regular intervals of time equal to T and the maximum displacement of the free ends at any instant is A. Write the equation of the standing wave.

View SolutionA point object O is placed on the principal axis of a convex lens of focal length 10 cm at 12 cm from the lens. When object is displaced 1mm along the principal axis magnitude of displacement of image is x1. When the lens is displaced by 1mm perpendicular to the principal axis displacement of image is x2 in magnitude. find the value of x1x2
View Solution
