Explain the parallel combination of resistors and derive the formula of equivalent resistance. Solution in Gujrati
Two or more than two resistors are said to be connected in parallel if one end of each resistor is connected to one point and the other end is connected to another point so that more than one paths are available for the current to flow and potential difference across each resistor is the same and is equal to the applied potential difference between the two common points.
Three resistors with resistances, R1,R2andR3 are connected in parallel between points A and B as shown in the figure 12.16 (a).
Here. the current I gets divided at point A amongst three resistors as shown in the figure.
The value of the current flowing through each . resistor depends on the value of its resistance.
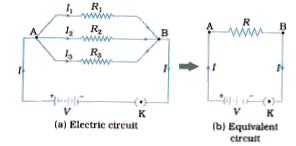
LetI1,I2andI3 be the currents flowing through the resistors with resistances R1,R2andR3 respectively.
∴I=I1+I2+I3 ... ... (12.12)
In a parallel combination of resistors, the potential difference across every resistor is equal < to the potential difference V of the battery. According to Ohm.s law,
I1=VR1,I2=VR2andI3=VR3
∴I1=VR1+VR2+VR3.......(12.13)
Now, if a resistor with resistance Rp, instead of three resistors with resistances R1,R2andR3, is connected in the circuit such that the current flowing through the circuit remains the same as I then Rp is called the eqUivalent resistance of the circuit [see figure (b)).
I=VRp ......(12.14)
From equation (12.13).
VRp=VR1+VR2+VR3
∴1Rp=1R1+1R2+1R3
Thus, in a parallel combination of resistors, the sum of the reciprocals of the individual resistances is equal to the reciprocal of the eqUivalent resistance Rp.Rp is less than any of ? the individual resistances in the circuit.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRICITYEXERCISE - QUESTIONS AND ANSWERS (INTEXT QUESTIONS)25videos
ELECTRICITY
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRICITYEXERCISE - QUESTIONS AND ANSWERS (TEXTBOOK ILLUSTRATIONS)14videos
ELECTRICITY
- BOOK - KUMAR PRAKASHANCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - VALUE BASED QUESTIONS WITH ANSWERS15videos
MAGNETIC EFFECTS OF ELECTRIC CURRENT
Similar Questions
What does an electric circuit mean?
04:56View SolutionA current of 0.5 A is drawn by a filament of an electric bulb for 10 minutes. Find the amount of eletric charge that flows through the circuit.
09:18View SolutionShalini and his brother Amey observed a water-pump working , Shalini inquired how an electric motor works . Amey collected different parts of an electric motor e.g., field - magnets , cabon- brushes , armature , battery , switch, connecting wire , split - rings , etc, and showed them to Shalini . Amey then explained how an armature could rotate.
State the principle how an electric motor to works .05:02View Solutionसमांतरक्रम में प्रतिरोधों को किस प्रकार संयोजित किया जाता है । इस संयोजन के लिए प्रतिरोधकों के समतुल्य प्रतिरोध का व्यंजक प्राप्त करें ।
08:40View SolutionExplain series and parallel combination of capacitors. Derive the formula for equivalent capacitance in each combination.
06:31View SolutionWhat is parallel combination of capacitors. Derive the formula for equivalent capacitance in parallel combination.
05:23View Solutionप्रतिरोधों के (i ) श्रेणीक्रम तथा (ii ) समान्तर - क्रम संयोजनों में तुल्य - प्रतिरोधों के लिए सूत्र स्थापित कीजिए तथा दोनों संयोजनों के निष्कर्ष लिखिए ।
06:31View SolutionExplain the equivalent resistance of a series and parallel resistor network.
06:31View Solutionप्रतिरोधों को समान्तर कर्म (पाश्र्वकर्म) में किस प्रकार जोड़ते है ? उनके तुल्य प्रतिरोध ज्ञात करने के सूत्र की स्थापना कीजिए |
View SolutionExplain the equivalent resistance of a series and parallel resistor network.
05:44View SolutionExplain the equivalent resistance of a series and parallel resistor network.
04:42View SolutionDerive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.02:30View SolutionWhat is parallel connection of resistors ? Derive equation of equivalent resistance in parallel connection.
02:22View SolutionDerive the formula of equivalent resistance of series combination of resistors.
02:56View SolutionDerive the equation of equivalent resistance of resistors connected in parallel.
04:05View Solution

