सम्मिश्र संख्याओं का मापांक, कोणांक तथा मुख्य कोणांक ज्ञात कीजिएः
a. z=1+cos10π9+isin(10π9)
b. (tan1−i)2
c.z=√5+12i+√5−12i√5+12i−√5−12i
The correct Answer is:(a) मुख्य कोणांक z=−4π9;|z|=2cos(4π)9; : कोणांक z=2kπ−4π9k∈I
(b) मापांक = sec21 , कोणांक z=2nπ+(2−π), मुख्य कोणांक z=(2−π)
(c) मुख्य कोणांक z=−π2 तथा |z|=32. कोणांक z=2nπ−π2,n∈I
मुख्यकोणांकz=pi/2तथा|z|=2/3,कोणांकz=2npi + pi/2, n in I
Step by step video, text & image solution for सम्मिश्र संख्याओं का मापांक, कोणांक तथा मुख्य कोणांक ज्ञात कीजिएः a. z=1+"cos"(10pi)/9+i sin ((10pi)/9) b. (tan1-i)^(2) c.z=(sqrt(5+12i)+sqrt(5-12i))/(sqrt(5+12i)-sqrt(5-12i)) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सम्मिश्र संख्या (COMPLEX NUMBER)BOOK - ALLEN HINDICHAPTER - सम्मिश्र संख्या (COMPLEX NUMBER)EXERCISE - EXERCISE-04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
10 Videos
- सम्मिश्र संख्या (COMPLEX NUMBER)BOOK - ALLEN HINDICHAPTER - सम्मिश्र संख्या (COMPLEX NUMBER)EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
3 Videos
- सम्बन्ध BOOK - ALLEN HINDICHAPTER - सम्बन्ध EXERCISE - EXERCISE-II
6 Videos
Similar Questions
माना z= x + iy एक सम्म्मिश्र संख्या है जहाँ x तथा y वास्तविक है। माना A तथा B समुच्चय द्वारा परिभाषित है A={z∣|z|≤2} तथा B={z∣(1−i)z+(1+i)¯z≥4} क्षेत्र A∩B द्वारा दर्शाया गया क्षेत्रफल ज्ञात कीजिये।
View Solutionदिए गए चित्र में |z|=r, त्रिभुज ABC का परिवृत है। D, E व F क्रमशः भुजाओं BC, CA तथा AB के मध्य बिन्दु हैं। AD आगे बढ़ाने पर वृत्त को L पर मिलाता है। यदि ∠CAD=0,AD=x,BD=y और त्रिभुज ABC का बिन्दु A से डाला गया शीर्षलम्ब, वृत्त |z|=r को M पर मिलाता है। यदि बिन्दुओं A,B तथा C के आगम क्रमशः za,zb तथा zc है-
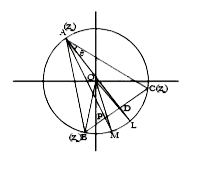
त्रिभुज ABC का क्षेत्रफल है -
View Solutionमानाकि R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} समुच्चय A = {1, 2, 3, 4} में एक संबंध है, तब संबंध R होगा-
View SolutionFind the conjugate of 1−i1+i
View SolutionSimplify: √5+12i+√5−12i√5+12i−√5−12i
View SolutionIf √5−12i+√−5−12i=z , then principal value of argz can be π4 b. π4 c. 3π4 d. −3π4
View Solution√5+12i+√5−12i√5+12i−√5−12i
View Solution√5+12i+√5−12i√5+12i−√5−12i=
View SolutionEvaluate: √5+12i
View Solution−5+12i
View Solutionनिम्नलिखित का मॉडुलस ज्ञात कीजिए:
−5+12i2+i
View SolutionIf z=(√5−12i+√−5−12i), then the principal value of arg z will be
View SolutionWhich of the following complex numbers is equal to (5 + 12i) − (9i2 − 6i), for i=√−1 ?
View SolutionThe imaginary number I is such that i2=-1. Which of the following options is equivalent to √5+12i ?
View Solution√−5+12i=
View Solutionसम्मिश्र संख्याओं का मापांक, कोणांक तथा मुख्य कोणांक ज्ञात कीजिएः
a. z=1+cos10π9+isin(10π9)
b. (tan1−i)2
c.z=√5+12i+√5−12i√5+12i−√5−12i
View Solution
