A particle of mass m and change q enter the region between two charged plates. The length of the plate is L and there is a uniform electric field 'E' between those plates as shown. Charge q enters into the field with an initial speed U as shown. Find the vertical deflection of the particle at the far edge of the plate?
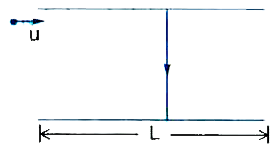
Here charged particle experiences force along vertical direction which is equal to Eq.
As a result its acceleration in the vertical direction is Eqm.
Along the horizontal direction, its velocity doesnot change.
Time taken by the charge to reach the other end of the plate is t=LU
During this time its vertical deflection is given by y=12at2
y=12Eqm(LU)2=EqL22mU2
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)
23 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-I)
18 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
10 Videos
Similar Questions
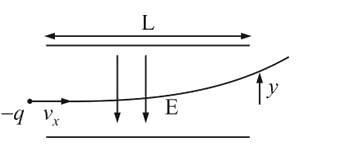
A paraticale of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx. The length of plate is L and a uniform electric field E is maintained between the plates. Show that the verticale deflection of the particle at the far edge of the plate is qEL2/(2mv2x). Compare this motion with motion of a projectille in gravitional field.
View SolutionA particle of mass m and charge(-q) enters the region between the two charged plates intially moving along x - axis with speed Vx . The length of plate is L and a uniform electric field E is maintained between the plates . Show that the verticles deflection of the particle at the far edge of the palte is qEL2/(2mv2x).
View Solution
Knowledge Check
A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircleA positive charged particle P enters the region between two parallel plates with a velocit u, in a direction parallel to the plates. There is a uniform electric field in the region. P emerges from this region with a velocit v. Taking C as a constant v will depend on u as
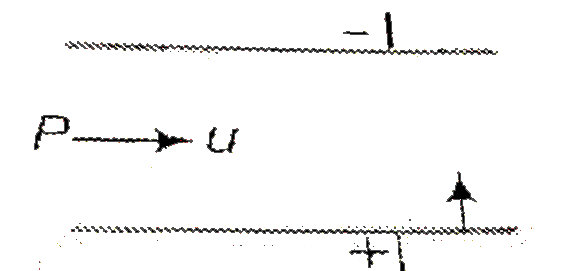 Av=CuBv=√u2+CuCv=√u2+CuDv=√u2+Cu2
Av=CuBv=√u2+CuCv=√u2+CuDv=√u2+Cu2A positively charged particle P enters the region between two parallel plates with a velocity u, in a direction parallel to the plates. There is a uniform electric field in this region. P emerges from this region with a velocity v. Taking C as a constant, v will depend on u as
 Av=CuBv=(√u2+Cu)Cv=(√u2+Cu)Dv=(√u2+Cu2)
Av=CuBv=(√u2+Cu)Cv=(√u2+Cu)Dv=(√u2+Cu2)
A particle of mass m and charge -q enters the region between the two charged plates initially moving along x-axis with speed vx as shown in figure. The length of plate is L and a uniform electric field E is maintained between the plates. The vertical deflection of the particle at the far edge of the plate is
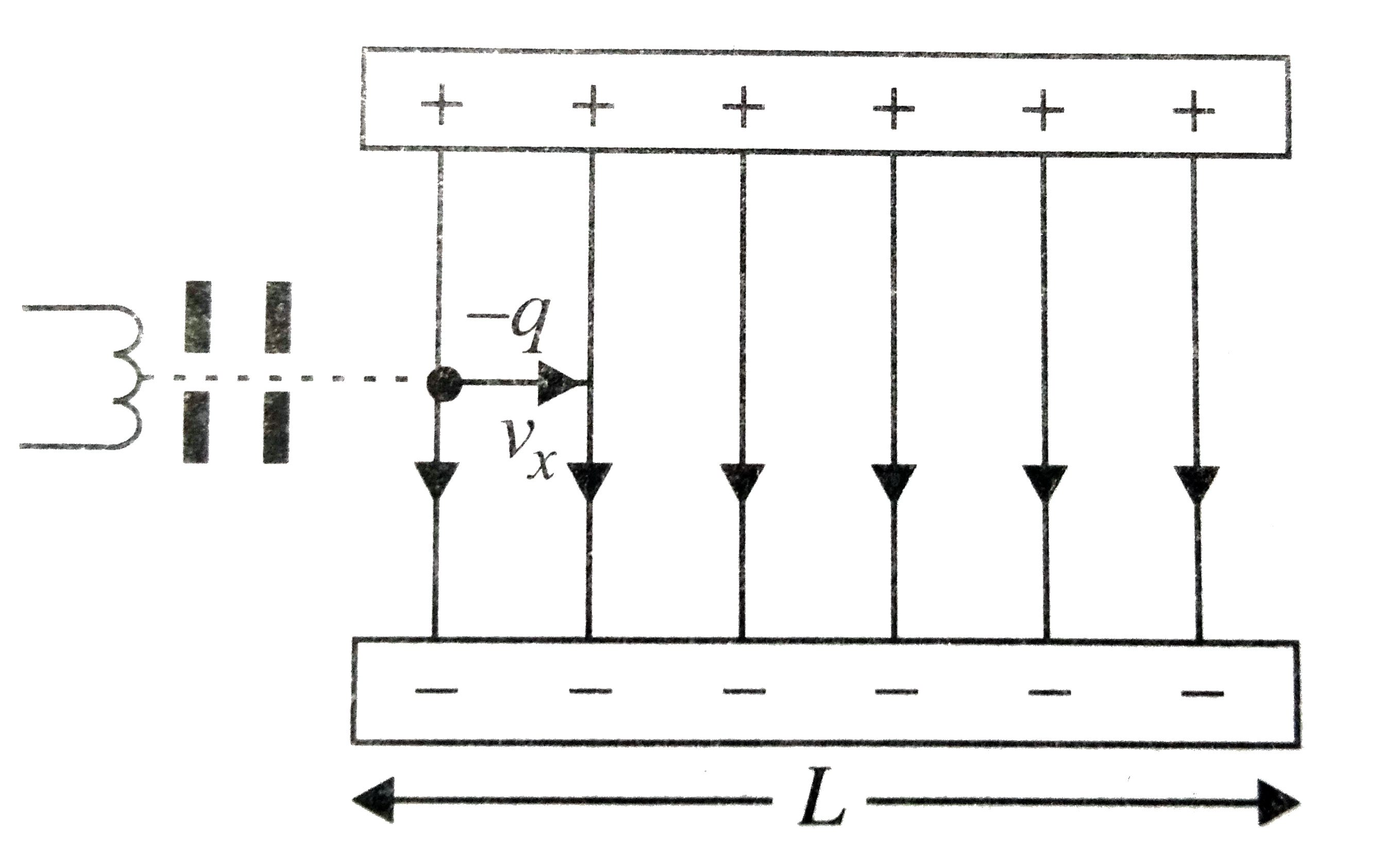
View SolutionA particle of mass m and charge (-q) enters the regions between the two charged plates initially moving along x-axis with speed vx (like particle 1 in.) The length of plate is L and an the particle at the far edge of the plate is qEL2/(2mv2x).
View SolutionA positively charged particle P enters the region between two parallel plates with a velocity u, in a direction parallel to the plates. There is a uniform electric field in this region. P emerges from this region with a velocity v. Taking C as a constant, v will depend on u as

View SolutionHow will the electric field between the plates in parallel plate capacitor change, if the charge on the plates is doubled?
View SolutionA particle of mass m and charge q enters a region of magnetic field (as shown) with speed v at t = 0. There is a region in which the magnetic field is absent as shown. The particle after entering the region collide elastically with a rigid wall. Time t after which the velocity of particle become antiparallel to its initial velocity is -

View Solution
