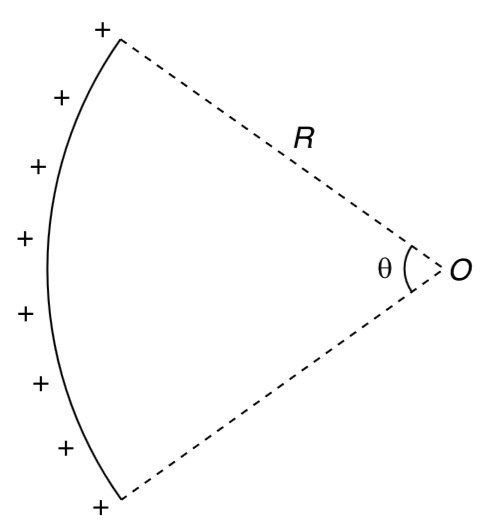
An arc of radius R and having a total charge Q has its charge uniformly distributed. The arc subtends an angle $2 θ$ at the centre O of the corresponding circle. Find the electric field intensity at O.

Text Solution

Verified by Experts

The correct Answer is: $\frac{1}{2 π \in_{0}} (\frac{Q}{R^{2} θ}) sin θ / 2$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-I)
18videos
ELECTRIC FIELD AND POTENTIAL
BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57videos
ELECTRIC CHARGES AND FIELDS
BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
10videos
ELECTROMAGNETIC INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
Charges $q$ is uniformly distributed over a thin half ring of radius $R$ . The electric field at the centre of the ring is
A $\frac{q}{2 π^{2} ε_{0} R^{2}}$
B $\frac{q}{4 π^{2} ε_{0} R^{2}}$
C $\frac{q}{4 π ε_{0} R^{2}}$
D $\frac{q}{2 π ε_{0} R^{2}}$
Question 2 - Select One
An arc of radius r carries charge. The linear density of charge is $λ$ and the arc subtends an angle $\frac{π}{3}$ at the centre.
A $\frac{λ}{4 ε_{0}}$
B $\frac{λ}{8 ε_{0}}$
C $\frac{λ}{12 ε_{0}}$
D $\frac{λ}{16 ε_{0}}$
Question 3 - Select One
An arc of length of length 19 cm of a circle of radius 30 cm, subtends an angle $θ$ at the centre O. The value of $θ$ is:
A $30^{\circ}$
B $37^{\circ}$
C $45^{\circ}$
D $52^{\circ}$

AAKASH SERIES-ELECTRIC FIELD AND POTENTIAL-PROBLEMS (LEVEL-II)

Home
Ask Doubt
Profile