Figure shows a semicircular ring of radius R with linear charge distribution λ given by λ=λ0sinθ. Find the electric field intensity at the centre of the ring.
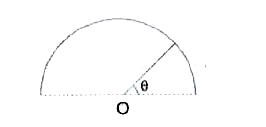
The correct Answer is:λ08∈0R
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-I)
Explore 18 Videos
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Exercise
Explore 57 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH SERIESChapter:ELECTROMAGNETIC INDUCTIONExercise:Additional Exercise
Explore 10 Videos
Similar Questions
A quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionConsider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View Solution
Knowledge Check
A rod with linear charge density λ is bent in the shap of circular ring. The electric potential at the centre of the circular ring is
Aλε0Bλ2ε0Cλε0D2λε0A semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
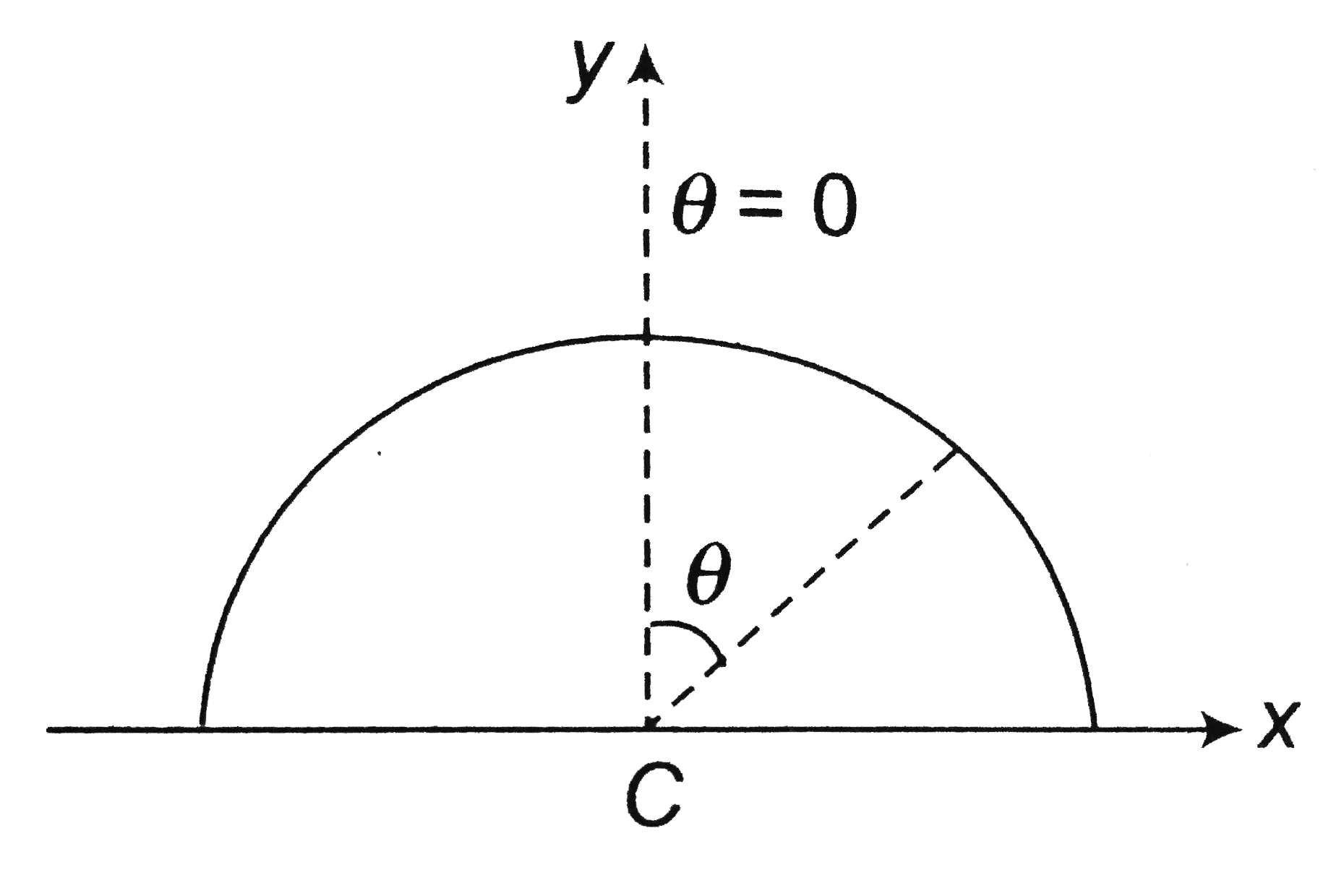 Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)
Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
A16B0C5D10
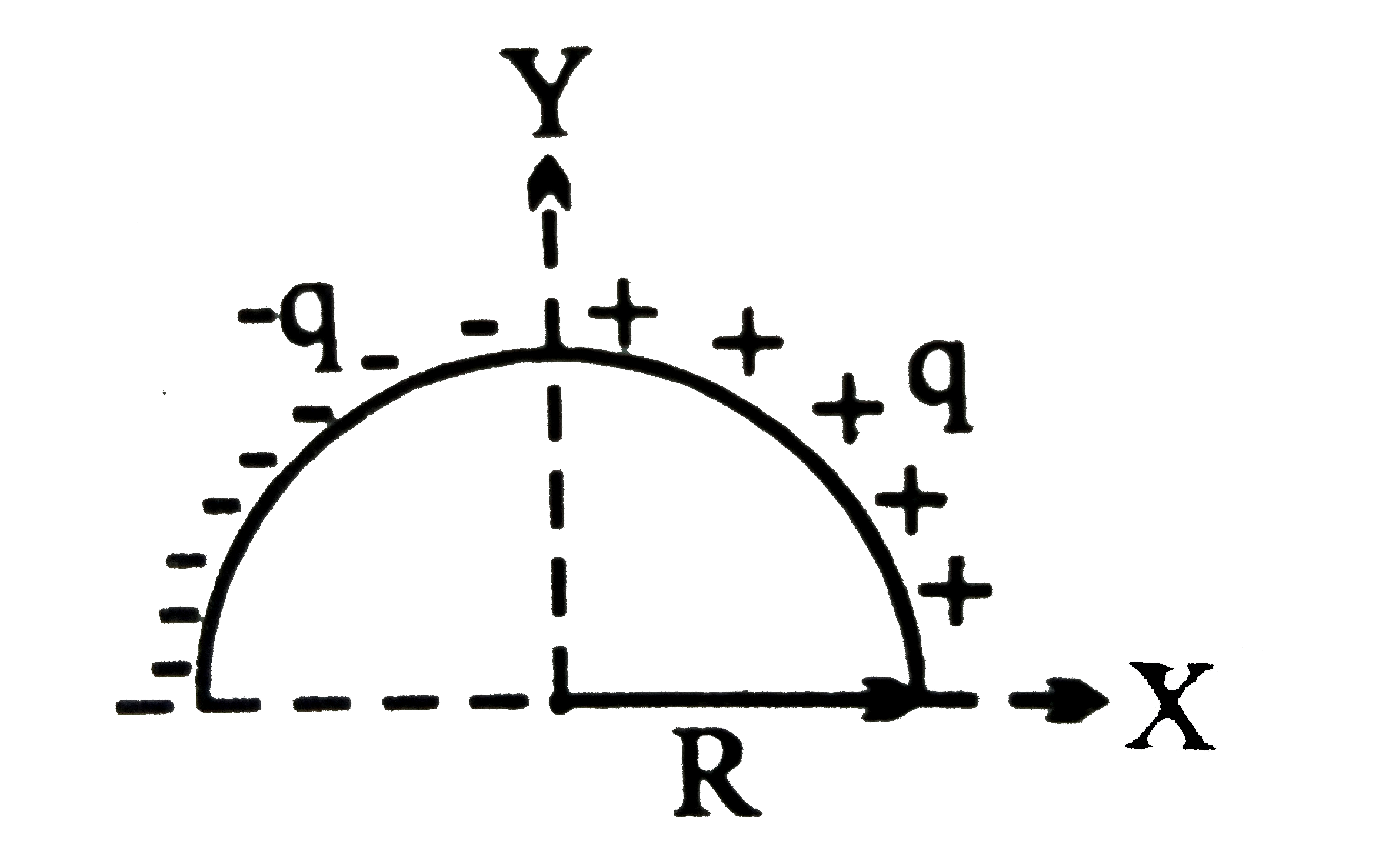
A ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionFind the electric field at centre of semicircular ring shown in figure .
 .
.
View SolutionFind the electric field at centre of semicircular ring shown in figure .
 .
.
View SolutionA semi-circular wire is charged with linear charge density dependent on the angle θ from +y -axis as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the center of the arc is ¯¯¯E=mKλ04R(−ˆj). Find m.(R is the radius of semi-circle and K=14πɛ0)
'(##CEN_KSR_PHY_JEE_C18_E01_033_Q18##)'
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View Solution
