A semi-circular wire is charged with linear charge density dependent on the angle θ from +y -axis as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the center of the arc is ¯¯¯E=mKλ04R(−ˆj). Find m.(R is the radius of semi-circle and K=14πɛ0)
'(##CEN_KSR_PHY_JEE_C18_E01_033_Q18##)'
The correct Answer is:4
Topper's Solved these Questions
Similar Questions
The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
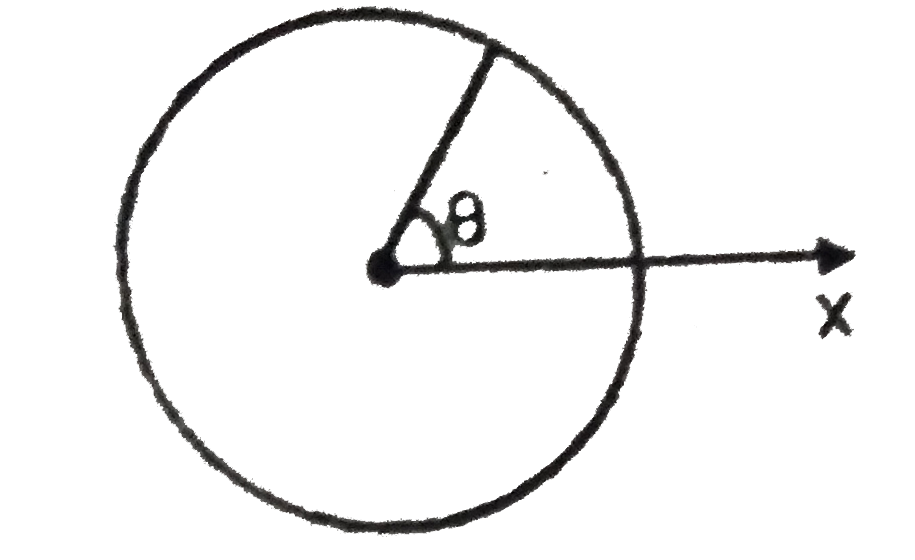
View SolutionThe linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View Solution
Knowledge Check
A semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
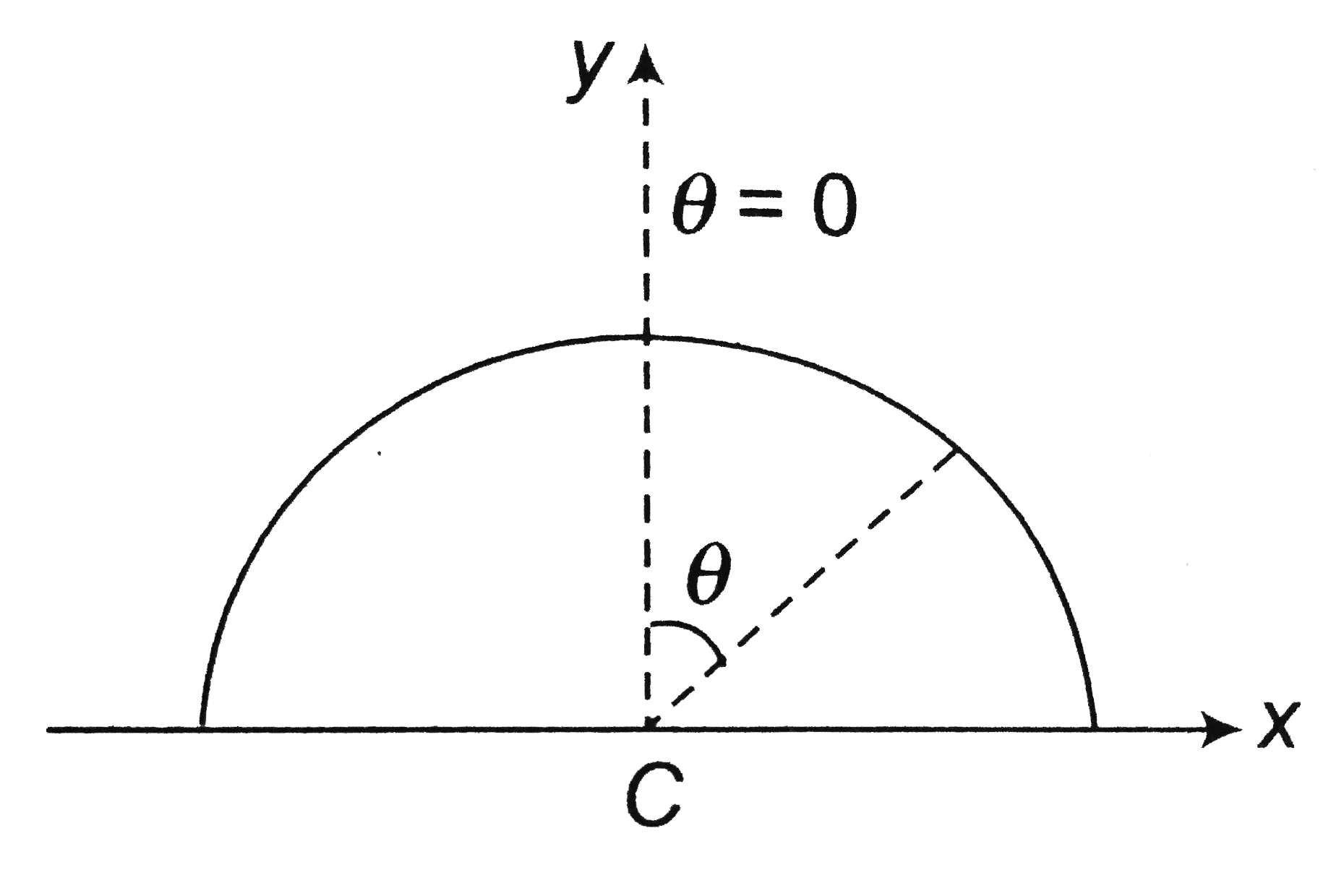 Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)
Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
A16B0C5D10the following diagram represents a semi circular wire of linear charge density λ=λ0sinθ where λ0is a positive constant.The electric potential at o is (take k=14πε0
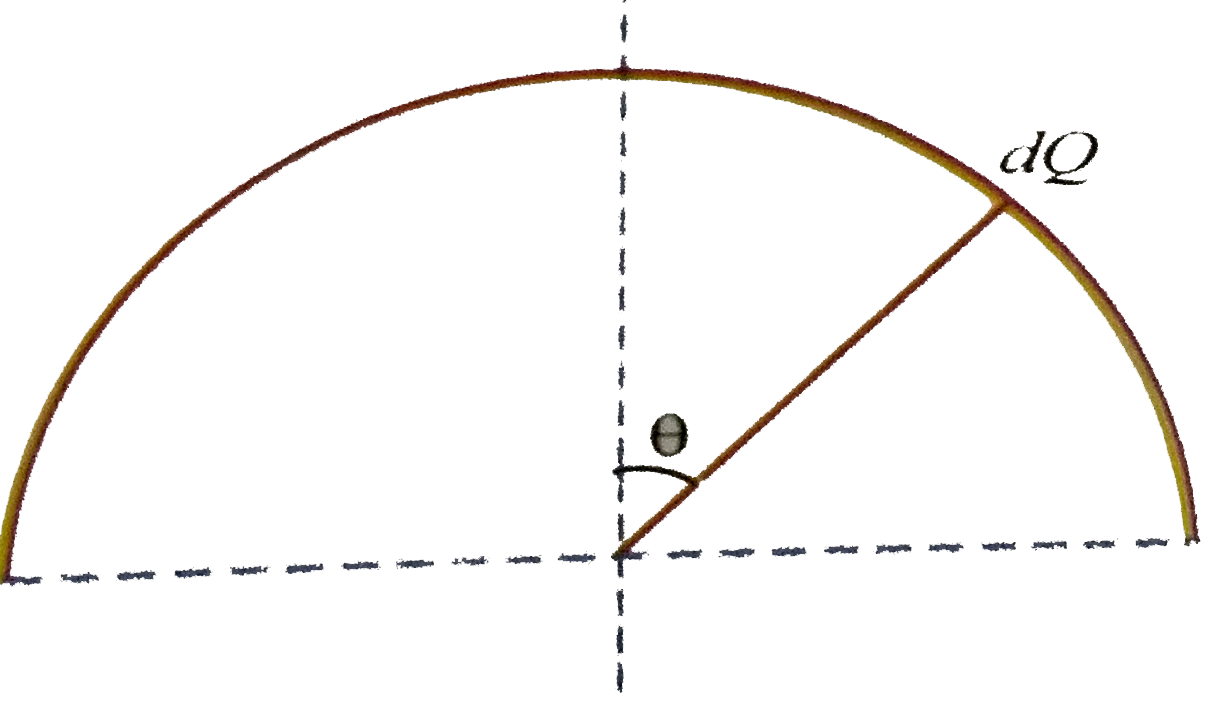 Akλ0sinθBkλ0cosθ2CzeroDkλ0cosθ
Akλ0sinθBkλ0cosθ2CzeroDkλ0cosθ
A circular wire of radius r has a uniform linear charge density λ=λ0cos2θ, The total charge on the wire is απλ0r2 Find α.
View SolutionA wire AMB is placed along y-axis having linear charge density λ C/m. The electric field intensity at point P is ( PM=0.1 m)
View SolutionThe linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is

View SolutionThe linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is

View SolutionA thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is

View Solution
