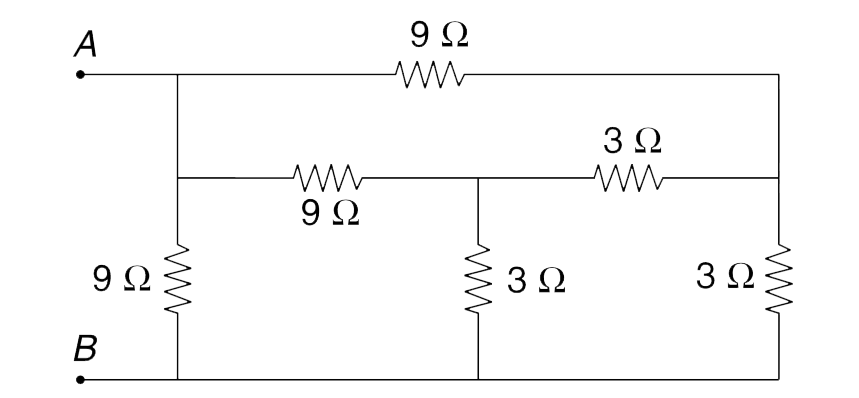
Find the equivalent resistance between the points A and B of the circuit shown in the fig.
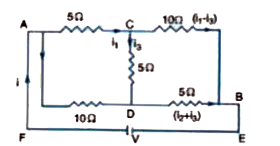
Text Solution
Supposing a source is connected between the terminals A and B . The current distribution is shown in fig.
At junction A , i=i1+i2
Resistance between A and B , RAB=Vi=Vi1+i2
In close loop ACDA, -5i1−5i3+10i2=0
or −i1−i3+2i2=0 .....(i)
In close loop C B D E
−10(i1−i3)+5(i2+i3)+5i3=0
or −2ii+i2+4i3=0 ....(3)
Now in close loop A C B E F A
−5i1−10(i1−i3)+V=0 or −3i1+2i3=−V5 .......(iii)
From equations (i) and (iii) , we get
−5i1+4i2=−V5 ......(iv)
From equations (ii) and (iii),
we get 4i1+i2=2V5 ...(v)
Solving equations (iv) and (v) , we get
i1=9V105
i2=6V105
i3=V35
RAB=Vi1+i2=V(9V105+6V105)+7Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
1 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - III
73 Videos
Similar Questions
Knowledge Check
The equivalent resistance between the points A and B in A the circuit shown in Fig. is
 A3.12ΩB1.56ΩC6.24ΩD12.48Ω
A3.12ΩB1.56ΩC6.24ΩD12.48Ω
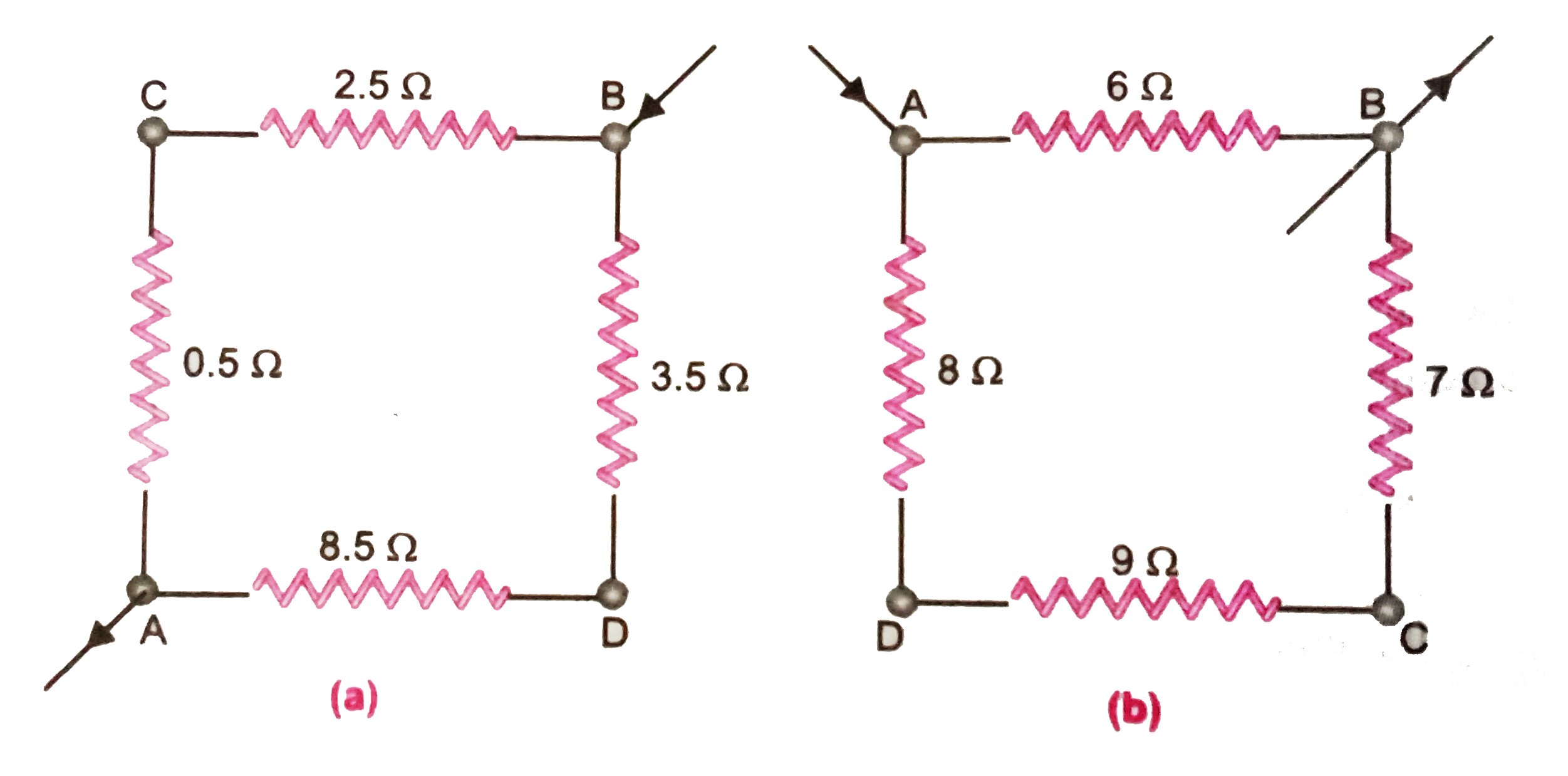
Calculate the equivalent resistances between the points AandB of the circuits shown in (fig. 2.33)(b).
 .
.
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionWhat is the equivalent resistance between points A and B in the circuit.

View SolutionCalculate the equivalent resistance between the points A and B in the circuit shown in Fig. (a)
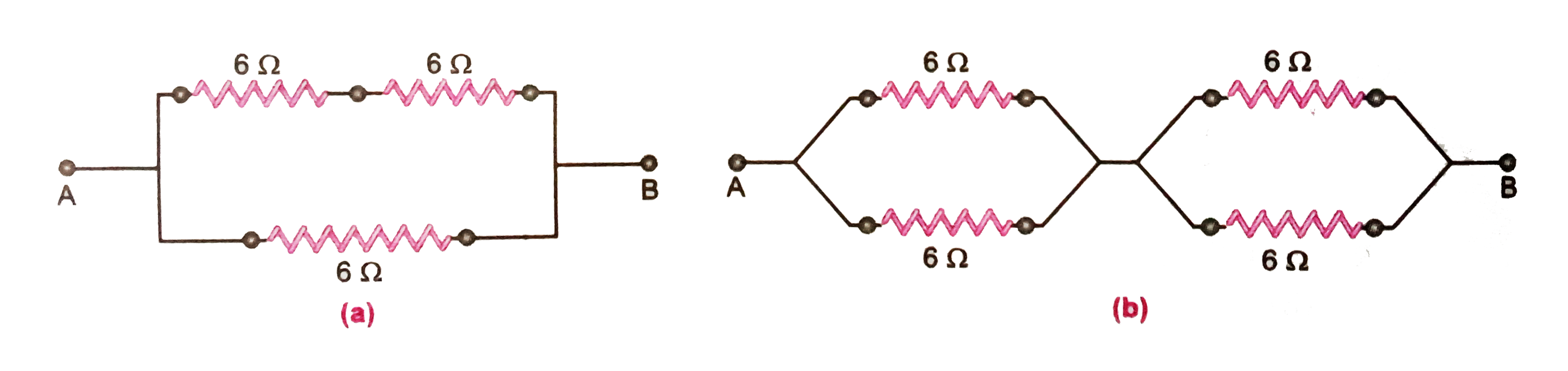
View SolutionCalculate the equivalent resistance between the points AandB in the circuits shown in (Fig. 3.19)
(a) and (Fig. 3.19) (b).
 .
.
View Solution